
如何将变形梯度张量极分解为SO(3)转动张量R和拉神张量U?这个看似简单的问题却在连续介质物理中有着至关重要的作用。经典的理论或采用直接求解的方法,然而由于SO(3)转动张量R的直接求解较为复杂,且难以以变形梯度张量F的形式直接表达。已有的研究也采用了一些显示的方法来尝试表达,但其提出的算法往往涉及特征值或张量的开方及取逆运算,形式复杂,不便理论分析和实际应用。
为了获得以变形梯度张量F表述的SO(3)转动张量R的简洁形式,我院孙博华院士基于凯莉-哈密尔顿定理,简化了直接求解的困难,首次给出了第一种(仅基于特征值的)旋转张量的显式、简洁表达式。其次结合任意旋转张量的指数映射,首次给出了第二种(仅基于位移梯度张量的)旋转张量的显式、简洁表达式,该表达式精确评估了Truesdell简单剪切变形的近似结果(图1),并认为Truesdell的结果非常准确(图2)。其中第一种表达式成功规避了张量开方及求逆的复杂运算,第二种表达式更在第一种的基础上成功规避了张量求特征值的复杂运算,相关成果已在《Applied Mathematics Letters》发表。
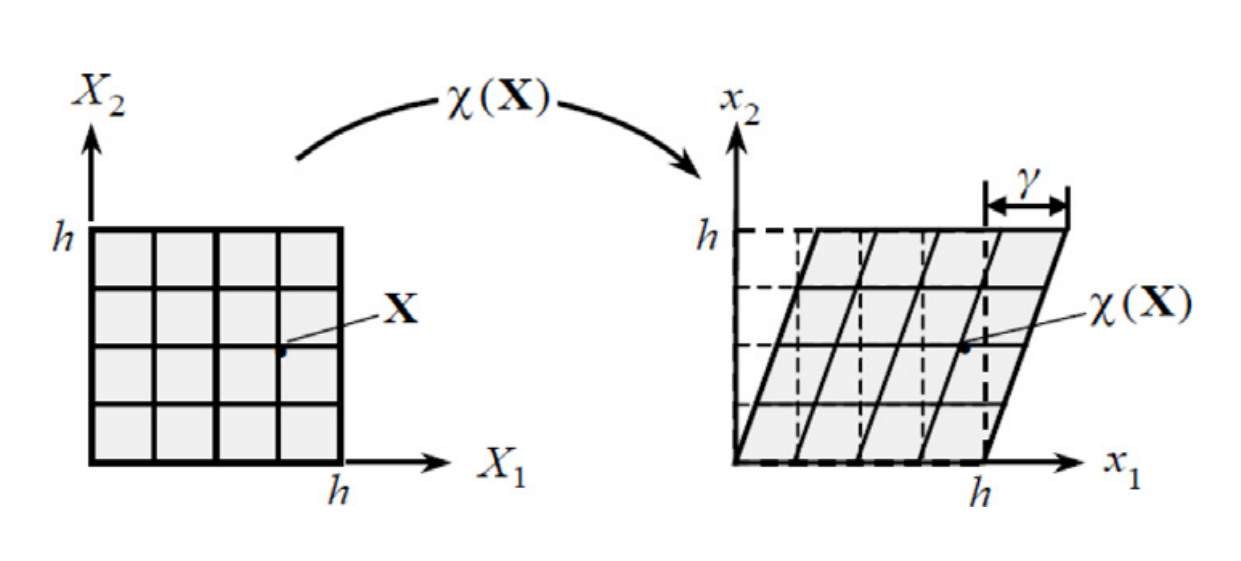
图 1.简单的剪切变形
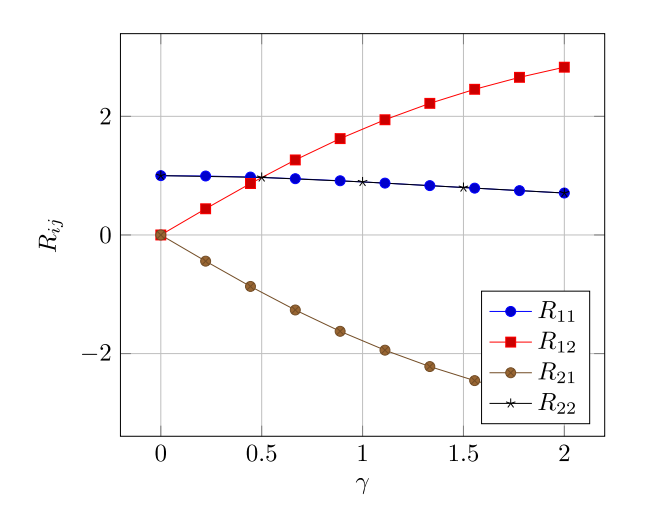
图2旋转张量分量和剪切变形的比较
《Applied Mathematics Letters》2021年影响因子为4.055,中科院分区1区top期刊。这篇论文以西安建筑科技大学为第一完成单位,孙博华院士为这篇论文的唯一作者。
论文链接:
Bohua Sun, Explicit representation for the SO(3) rotation tensor of deformable bodies, Applied Mathematics Letters, 111 (2021) 106606
https://doi.org/10.1016/j.aml.2020.106606