格子Boltzmann方法助力微尺度流动研究

格子Boltzmann方法助力微尺度流动研究

随着人们对微观世界的一步步深入认知，发现微观世界与已知的宏观宇宙有许多相似之处，比如可以把各个星系看成是一个个原子和分子，中心高质量的恒星是原子核，围绕它的是电子。微观宇宙的概念常常出现在各类科幻作品中，如刘慈欣的科幻小说《三体》中提到的隐藏在质子中的微观文明，可跨越维度反击三体文明；再如漫威出品的电影《蚁人2》(2018)中的量子领域，在逐步进入这个微型空间的过程中可看到水熊虫等微型生物（图1）。微观世界如同宏观宇宙一样，一直以来都在激起人们探寻世界的欲望。

图1 《蚁人2》中的水熊虫

在物理学中，物质的宏观尺度行为与微观尺度行为密切相关。在研究流体的运动规律时也是如此，例如，如果可以掌握流体分子的运动规律，那么就可以得知流体的宏观运动规律，这就是分子动力学的研究思路。然而，目前的人类的计算能力无法承受我们从分子角度去考虑所有的问题，1753年瑞士著名科学家欧拉提出一个比较现实的方法是将流体当作连续介质对待，这就是著名的“连续介质假设”，并提出描述理想流体的基本方程——欧拉方程。之后科学家们经过近百年的努力提出了描述粘性可压流体运动的“纳维尔-斯托克斯(Navier-Stokes, N-S)方程”(1845)。套用《指环王》的故事，N-S方程可以比做至尊魔戒，其它大大小小的方程比做各个流体力学国度国王拥有的普通戒指，那么可谓是一戒统领众戒 (one ring rules all rings)。如今N-S方程已经渗透到描述流体的方方面面，也在众多实际工程中得到了应用。但是，这个方程的数学特性——解的存在性和光滑性至今没有得到证明，这个问题也是美国克雷数学研究所（Clay Mathematics Institute）在2000年提出的7个千禧年大奖难题中的问题之一。由于一般工程问题中N-S方程求解的困难性，我们往往需要追求其近似解，因此计算流体力学(CFD)在当今工程领域扮演着重要角色。CFD通过计算机数值求解N-S方程可重现流体的运动规律，已成为科学家手中的利器。

在众多CFD方法中，格子Boltzmann方法（Lattice Boltzmann Method, LBM）由于独特的物理背景和简单的实现手段近几十年来逐渐成为人们关注的焦点。LBM的微观本质及其介观粒子特性可直观、方便地处理流体内部及流体与周围环境的相互作用，从而对复杂流动系统的分析具有较大的优势。例如，可以通过粒子的反弹来描述流体与壁面的相互作用，更容易处理复杂的运动边界；固定的格子网格大大降低了计算成本，同时由于其演化过程的区域性，LBM具有天然的并行性，能够胜任大规模的计算量。LBM已经在湍流、多相和多组分流、粒子悬浮流、反应燃烧系统、磁流体力学、微尺度流动等领域取得了很大的进展。

然而，连续介质假设掩盖了一些微尺度的物理现象，如布朗运动。由于连续介质假设给出流体质点（微团）的概念，需要在微观上足够大，流体质点里面包含着许许多多分子，其行为已经表现出大量分子的统计学性质，分子热运动的差异性被忽略了，因此这种“平均”的做法无法描述由分子热运动导致的微颗粒的布朗运动。1959年，前苏联全能物理学家、诺贝尔物理学奖获得者朗道(Landau)在N-S方程基础上建立了涨落动力学方程，引入随机应力项来描述流体分子热运动导致的动量和能量涨落。随着CFD、LBM的兴起，1993年Ladd将涨落动力学引入LBM中，成功的模拟了微颗粒的布朗运动【Ladd, A.J., Short-time motion of colloidal particles: Numerical simulation via a fluctuating lattice-Boltzmann equation. Physical review letters, 1993. 70(9): p. 1339.】。从此涨落格子Boltzmann(FLB)方法被逐步用于研究微颗粒的复杂运动。

针对这类问题，崔海航、陈力所在科研团队，发展了一种可以直接模拟非平衡态颗粒运动的方法。针对自驱动颗粒复杂的运动和多时间尺度模拟需要的巨大计算资源，在FLB基础上混合网格加密技术，成功应用FLB方法复现了球形自驱动微颗粒在双氧水中的运动特性，并预测了圆柱形微颗粒可能存在的运动规律（图2），为研究自驱动微颗粒的在复杂条件下的运动规律开辟了一种新的CFD方法。

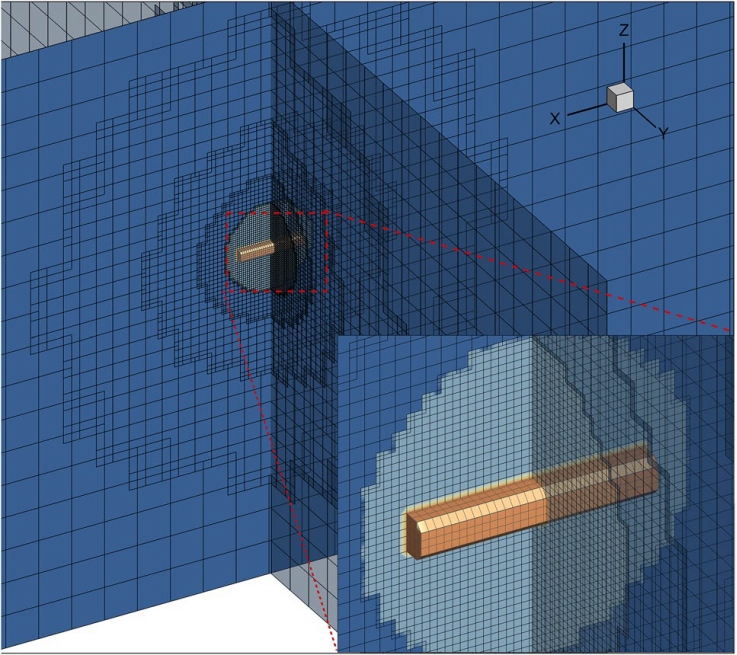
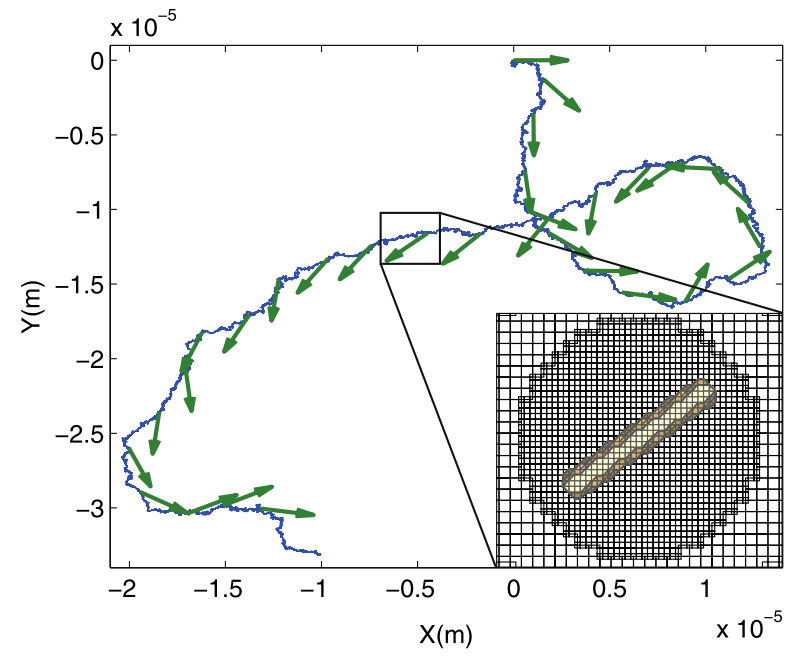
图2 圆柱形微颗粒的网格及运动轨迹

论文及链接:

Li Chen, Chenyu Mo, Lihong Wang and Haihang Cui, Direct numerical simulation of the self-propelled Janus particle: use of grid-refined fluctuating lattice Boltzmann method. Microfluidics and Nanofluidics, 2019. 23(5): p. 73.

https://link.springer.com/article/10.1007/s10404-019-2230-1