有歌曲:
这一天 我开始仰望星空 发现
星并不远 梦并不远 只要你踮起脚尖
我相信有一双手把我轻轻牵到你的跟前
我相信有一根线将梦想与现实相连
我相信有一种缘会把所有的偶然都实现
…………

图1:神秘广袤的宇宙一直启发人类的理性思维
近年来,有关宇宙研究的好消息不断传来,从2016年2月11日LIGO合作组宣布首次直接探测到来自遥远宇宙中的引力波(图2),到2019年4月11日全球同步发布“黑洞“的第一张照片(图3)。
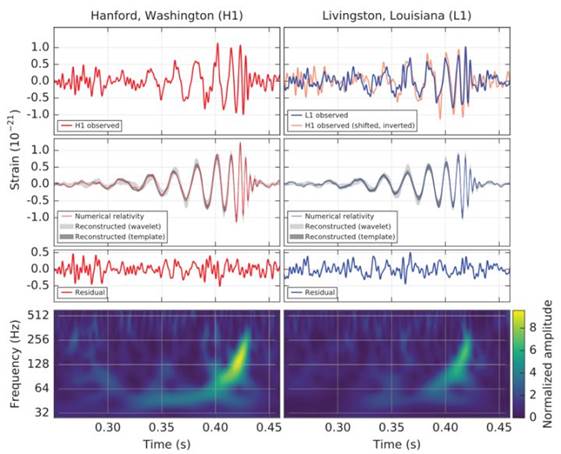
图2:人类第一次直接探测到引力波,LIGO的GW150914 (B.P.Abbott et al. 2016)

(a)

(b)
图3:(a) 黑洞的第一张照片, (b) 有关黑洞的一些定义
再到刘慈欣创作的系列长篇科幻小说《三体》,讲述了地球人类文明和三体文明的信息交流、生死搏杀及两个文明在宇宙中的兴衰历程;和根据刘慈欣同名小说改编《流浪地球》电影,故事设定在2075年,讲述了太阳即将毁灭,已经不适合人类生存,而面对绝境,人类将开启“流浪地球”计划,试图带着地球一起逃离太阳系,寻找人类新家园的故事。这些科学和科幻中迷人故事都再次极大地引起了人们对宇宙奥秘的兴趣。
人类有关宇宙的研究开始于对地球、月亮和太阳运动的研究。 从托勒密的“地心说”到哥白尼的“日心说”,科学与宗教的千年激烈辩论是人类思想发展的壮丽诗篇。其中的三体问题,即太阳-地球-月亮,是其中的主旋律。
在二十世纪的第一次数学家大会(1900 年) 上, 二十世纪伟大的数学家希尔伯特(David Hilbert)在他著名的演讲中提出了23个困难的数学问题,这些数学问题在二十世纪的数学发展中起了非常重要的作用。在同一演讲中,希尔伯特也提出了他所认为的完美的数学问题的准则:问题既能被简明清楚的表达出来,然而问题的解决又是如此的困难以至于必须要有全新的思想方法才能够实现。为了说明他的观点,希尔伯特举了两个最典型的例子:第一个是费尔马(Pierre de Fermat)猜想,即代数方程x^n+y^n=z^n 在n大于2时是没有整数解的;第二个就是我们这里介绍的N体问题的特例------三体问题。 费尔马猜想经过全世界几代数学家几百年的努力,终于在1994年被美国普林斯顿大学(Princeton University)威尔斯(Andrew Wiles)最终解决,这被公认为二十世纪最伟大的数学进展之一。
正象希尔伯特指出的,费尔马猜想的产生来源于纯粹的数学思维,而N体问题则来源于天体力学,对它的认识也有助于人类对自然界最简单的基本现象的理解。N体问题可以用一句话写出来:在三维空间中给定N个质点,如果在它们之间只有万有引力的作用,那么在给定它们的初始位置和速度的条件下,它们会怎样在空间中运动。最简单的例子就是太阳系中太阳,地球和月球的运动。在浩瀚的宇宙中,星球的大小可以忽略不及,所以我们可以把它们看成质点。如果不计太阳系其他星球的影响,那么它们的运动就只是在引力的作用下产生的,所以我们就可以把它们的运动看成一个三体问题。我们知道地球和月球都在进行一种周期性运动,这样我们才有了年,月和日的概念。所以大家不难想象周期运动可能是三体问题的一种解。然而对N体问题的全面认识就不是那么简单了,数学家几百年以来的研究证明各种千奇百怪的运动都有可能在N体问题中出现。
当 N=1 时,单体问题是个平凡的方程。单个质点的运动轨迹只能是直线匀速运动。当 N=2 的时候 (二体问题),问题就不那么简单了。但是方程组仍然可以化简成一个不太难解的方程,优秀的理科大学生大概都能轻易解出来。简单来说这时两个质点的相对位置始终在一个圆锥曲线上,也就是说如果我们站在其中一个质点上看另一个质点,那么另一个质点的轨道一定是个椭圆,抛物线,双曲线的一支或者直线。二体问题又叫开普勒(Johannes Kepler)问题,它是在1710年被瑞士数学家约翰伯努利(Johann Bernoulli) 首先解决的。N体问题的提出大概可以追溯到上千年前,但是这一问题的第一个完整的数学描述(象使用上面这样的微分方程)是出现在牛顿的“自然哲学的数学原理”(Philosophiae Naturalis Prinicipia Mathematica,1687年出版)一书中。
至于三体问题或者更一般的N体问题(N大于二),在被提出以后的二百年里,被十八和十九世纪几乎所有著名的数学家都尝试过,但是问题的进展是微乎其微的,人们期待重大突破的出现......
最早系统研究三体问题的是法国数学家,物理学家庞加莱(Jules Henri Poincare), 为此他于1885年提出了动力系统的定性理论和最早“混沌论”的雏形。但定量的研究周期轨道自1885年以来都没有特别的进展,后来借助于计算机的发展有了突破性进展,于1993发现8字型的周期轨道【C. Moore, Phys. Rev. Lett.70, 3675 (1993).】,2013年发现13类周期轨道【M. Suvakov and V. Dmitrasinovi_C, Phys. Rev. Lett.110,114301 (2013).】,和2017年廖世俊课题组发现的2千多类周期轨道【X.M. Li and S.J. Liao, Sci. China-Phys. Mech. Astron.60, 129511 (2017).】。
可以预料,三体的周期轨道有无穷多类,那么我们就有一个问题,这么多的周期轨道是否也有二体系统的开普勒第三定律,是否存在不变量,即开普勒周期律?廖世俊课题组在大量数值模拟的基础上对于特殊情况提出了一种线性周期律,但由于问题太复杂,对于不等质量的三体周期轨道,还没有相应的结果。
孙博华于2018年根据量纲分析和引力质量乘积的对称性,给出了一个三体和N体的开普勒周期律的猜想【B.H. Sun, Kepler’s third law ofn-body periodic orbits in a Newtonian gravitation field, Sci. China-Phys. Mech. Astron.61, 054721 (2018)】。这篇文章发表后,由于其研究问题的重要性和思路的新颖性,立刻引起了有关著名学者的关注。著名力学家北京大学佘振苏教授和国家紫金山天文台的天体力学家 Chang-Yin Zhao,Ming-Jiang Zhang,分别发表专文高度评价孙博华的研究成果,预测将对于宇宙的探索有重要的意义【Z.-S. She, Kepler’s third law of N-body system, Sci. China-Phys. Mech. Astron.61, 094531 (2018), https://doi.org/10.1007/s11433-018-9221-y;Chang-Yin Zhao,Ming-Jiang Zhang,A conjecture on Kepler's third law of n-body periodic orbits,arXiv:1811.00735[physics.class-ph] https://arxiv.org/abs/1811.00735v1】。
特别要指出的,近来比利时物理学家 C.Semay 说量子理论也支持孙博华的猜想【1.Semay C. Quantum support to BoHua Sun’s conjecture; 2018. arXiv:1812.00807v2.;2. Semay C.Quantum support to BoHua Sun’s conjecture;Results in Physics 13 (2019) 102167 https://doi.org/10.1016/j.rinp.2019.102167】
2019年初,孙博华院士又把其结果推广到质量不等的量子系统 【Bohua Sun,Classical and quantum Kepler’s third law of N-Body System,Results in Physics 13 (2019)102144 https://doi.org/10.1016/j.rinp.2019.02.080】