力学家访谈录：冯朝刚教授

2023年6月14日17:00，由西安建筑科技大学力学技术研究院（IMT）开展的力学家访谈，在IMT成功进行。本期访谈的嘉宾是淡江大学冯朝刚教授。  

访谈掠影

力学家访谈源于对力学家的致敬，希望以访谈的形式请他们分享自己的学术成果、科研心得、新思想，以此激励学生的科学研究激情。采访内容如下：

问：量纲分析和相似法在力学中的基本原理是什么？

答：工程科学的理念，首先是对探讨的问题要有正确的物理感受(Feeling)，然后才能经由数学估算(Estimation)出较准确的结果。任何一个物理问题中的物理量是由基本量纲(Dimension)所组成，对于一个复杂的问题不容易建立其正确之数学模型，或者因问题建模的方程式困难而难以求解，此时，运用“量纲分析”则可得出其定性关系式，再配合理论方法或实验方法得以求出其规律性。“量纲分析”有两种方法，(1) Rayleigh’s Method，他是将物理问题中的因变物理量Q₀与自变物理量Q₁, Q₂,…, Q_n之间以幂次律表达为     ，其中k为待求之常数，而α₁, α₂,…, α_n为待求之指数以使得上述等号左右之物理量具有相同之量纲。(2) Buckingham π-Method，本方法指出，当一个物理上有意义的问题，其中有n个物理量，而这些物理量由r个独立的量纲所组成，则该物理问题可简化成p=(n-r)个无量纲参数π₁,π₂,_…,π_p组成的方程式（此处的r可以由所有物理量之量纲所组成特定矩阵的秩而得出），而这些无量纲参数是由原问题中的物理量所组成。

本人在此次学术报告中所提出之相似法，是探讨力学问题之一种重要的解析方法，它是指力学问题中对应有多自变数之偏微分方程式数学模型，以探讨其具有相似变换解(Similarity Solution)之方法。所谓相似变换(Similarity Transform)，直观而言，是指一个具有n个自变数的偏微分方程式，经由某种坐标转换组合成(n-1)个自变数。例如当n=2时，经过坐标变换成1个自变数，则该偏微分方程式可转换成一个常微分方程式，如此则较为容易求解。当物理问题具有良好之边界形状和适当之边界条件，则有可能得出全域之相似解，但实际工程或力学问题之边界形状和边界条件并不简单，而无法求出全域相似解，但此时仍有可能在问题中之局部(Local)有所谓局部相似解，或在远场处(Far Field)有所谓远场相似解。有关量纲分析和相似法之详细方法和内容，请参考孙博华院士著作“量纲分析与Lie群”。

问：相似法是什么？它与量纲分析有何关联？在相似性分析中，我们如何确定哪些物理量是重要的，哪些可以忽略，以建立相似性关系？

答：本人学术报告中的相似法是指力学问题中的偏微分方程式，经由某种坐标变换而使其自变数合并而减少的一种变换，即所谓相似变换。现以二维拉普拉斯方程式     为例加以说明，设稳态温度     ，其中T₀为常数，     为相似变数而 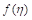    则适合一个二阶常微分方程式，例如由Lie群转换得知有(1)伸缩群    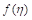 ，     所适合之常微分方程式为     ，(2)旋转群    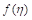 ，     所适合之常微分方程式为     ，(3)反演群    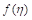 ，     所适合之常微分方程式为     。上述(1)中之伸缩群变换     就是一个无量纲的相似变数，换言之，量纲分析法所提出之无量纲参数（或无量纲变数）只是相似变换法中最基本伸缩群的一个特例，然而相似法中之伸缩群变换与量纲分析法在探讨工程和力学问题中却占有重要的地位。二者方法所得出之结果，也是最容易体现出问题中其数理结构之本质。有关如何确定问题中哪些物理量是最重要的，哪些是可以忽略的，这是需要靠对问题之物理特性要有深入和正确的了解，这些都是需要经验并使用实验法来验证所得之结果，以建立正确之量纲分析和其相似性关系。

问：在实际应用中，量纲分析和相似法可能会遇到哪些挑战和限制？如何克服这些问题以确保方法的有效性和可靠性？

答：任何一个实际的工程或力学问题其处理之步骤是要经过理想化(Idealization-Physics)及近似化(Approximation-Mathematics)之处理，以建立正确之模型而求得其近似解。尤其是新的科学问题，由于问题本身可能还没有完全了解或确定，采用量纲分析和相似法处理时，会受到限制和挑战。有关物理问题中如何选择适合之物理量，在大英百科全书有关量纲分析条目中，引用了物理大师爱因斯坦对此问题有一段说明：“如果量纲分析中物理量选择正确，则所得出结果中之常数会是一个既不很大，也不会很小的常数”，这是一段很富有哲理的话，同时也道出了物理世界之奥秘！当然采用量纲分析和相似法所得出的结果，须经由理论方法，实验方法和数值方法相互验证，才能确保其结果之有效性和可靠性。

采访：刘哲
撰稿：刘哲