日常生活中,可以看见路边的树木在强风中弯曲,从而吸收变形能并减少风对树木的阻力(如图1所示)。这种自然现象启发人们使用可变形的物体来设计流线型形状,并且可以减少相应的阻力。寻找气动外形和减阻是空气动力学中二个相互交织的重要问题。在以往的研究中,Alben, Shelly和Zhang(张俊)【S. Alben, M. Shelley and J. Zhang, Drag reduction through self-similar bending of a flexible body, Nature 420, 479-481 (2002)】报道了在流动介质中浸泡的柔性体通过形状重构减少阻力的实验和理论研究结果,他们总结得到的规律可以被称为Alben-Shelley-Zhang标度律。然而,Alben, Shelly和Zhang也留下了一个有趣的未解问题,即他们的标度律是否是普适的?研究人员在这里使用量纲分析方法,得到了一个通用的阻力标度律并验证了Alben-Shelley-Zhang标度律的普适性,获得的普适规律对气动流线型设计和减阻具有重要意义。

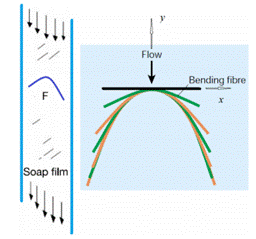
图1树在风中弯曲和模型(将纤维(F)插入到流动的肥皂膜流道)
针对这问题,西安建筑科技大学力学技术研究院孙博华教授团队开展了流动介质中柔性纤维的气动形状和阻力标度律研究。相关工作于以“Aerodynamic shape and drag scaling law of a flexible fibre in a flowing medium”为题发表在力学期刊《Theoretical and Applied Mechanics Letters》。

我们知道,任何物理关系都可以以无量纲的形式表达。量纲分析是一种通用的方法,因为它没有任何明确的考虑可能支配一个物理现象的控制方程和边界条件。因此,学术界存在共识,认为普适性可以通过量纲分析来实现。如果一个规律可以通过量纲分析的检验,就可以认定它是普适的规律。
Alben-Shelley-Zhang阻力标度律是普适的吗?为此他们使用量纲分析方法来检查这个问题,而不进行使用任何方程做任何特定的具体计算。
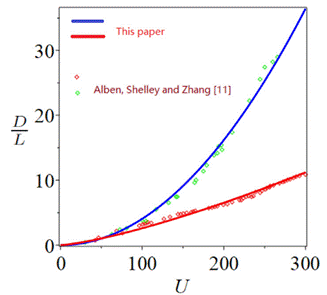
图2柔性纤维的单位纤维长度D/L与流速U的关系
经过细致考察,Alben-Shelley-Zhang标度律的普适性成功通过量纲分析验证。从而得到,对于流动介质中的柔性纤维,广义的阻力标度律或广义的Alben-Shelley-Zhang标度律是
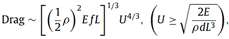
这里的研究和理解对于流线型设计和减少阻力具有重要意义。
论文第一作者为西安建筑科技大学土木工程学院和力学技术研究院孙博华教授,第二作者为西安建筑科技大学土木工程学院2022级结构工程专业博士研究生郭晓琳。
原文链接:https://doi.org/10.1016/j.taml.2022.100397
力学人连接:https://mp.weixin.qq.com/s/X3jTTb0WWqXRKopoepgVhg