
受到挤压的皮肤为什么会起皱纹?风干的水果表皮为什么会凹凸不平?两种不同刚度和厚度的软膜粘贴组合在一起,在挤压作用下的表现却揭示了一个广泛存在于自然界中,但长久被人忽视的现象,即褶皱的发生。近期,这个问题越来越多的引起了大家的广泛注意。人们逐渐意识到这种双层膜结构广泛存在于自然环境中,如生物上表皮和真皮组成的平面双层膜结构、大分子物质的硬表面和内部组成的球形双层膜结构、地质结构中的岩层和土层形成的大尺度双层膜结构等等。
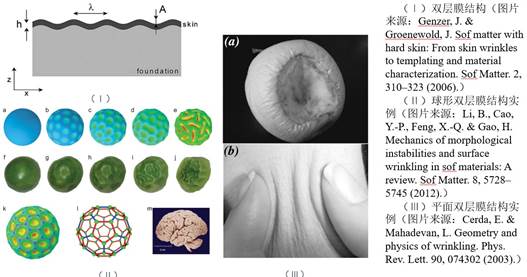
图1、双层膜结构实例
如今,薄膜-软基双层结构已经成为软物质领域研究的热点之一。一般认为,在持续的压缩荷载作用下,较硬的薄膜与较软的基体存在弯曲变形的趋势,二者自身变形的趋势在竞争过程中将趋于使得总体变形能最小,并在薄膜表面产生初步的褶皱现象,这种褶皱在一定情况下保持稳定。而进一步增加荷载直到超过临界后,稳定的平衡再次被打破,薄膜的表面形成新的形态,即后屈曲模式,并且这种后屈曲模式同样会在进一步荷载作用下继续被打破。在考虑基体厚度无限大的情况下,学者们已经很好的总结了若干屈曲模式,如图2所示。
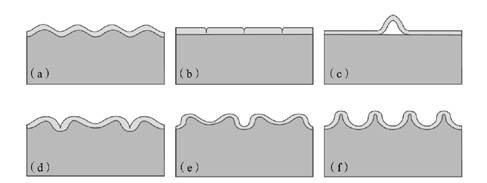
图2、典型的屈曲失稳模式示意图,从(a)-(f)依次为褶皱、折痕、翘曲、叠痕、倍周期褶皱、隆起(图片来源:倪勇, 刘佩琳, 马龙,等. 基底上薄膜结构的非线性屈曲力学进展[J]. 固体力学学报, 2018, 39(2):26.)
目前的研究仍将薄膜折叠后作为后屈曲的终点,并且研究往往聚焦于薄膜厚度相比基体厚度即膜厚比较大的情况,此时基体被视为半无限大弹性空间,因而给理论的解析带来了方便,无限大基体的后屈曲失稳路径为典型的褶皱-倍周期-四倍周期模式。然而有限厚度下的薄膜-软基体复合结构在自然界中往往更加广泛的存在,当考虑基体厚度时,这种双层膜的后屈曲研究更是尚不充分。
鉴于此,西安建筑科技大学力学技术研究院孙伯华教授团队受到复旦大学徐凡教授团队对于双层膜后屈曲研究(Cheng, Z. & Xu, F. Intricate evolutions of multiple-period post-buckling patterns in bilayers. Sci. China Phys. Mech. Astron. 64, 1–10 (2021).)的启发,通过考虑基体厚度,和薄膜表面折叠后的接触滑移,采用有限元数值方法,发现了新的屈曲路径,即将原来的单一屈曲路径(无限大基底情况下)拓展为五种。并且在不考虑摩擦力的情况下,发现了薄膜接触后的进一步屈曲演化模式(路线四,对称性破缺后重新分布情况)。相关工作于2022年以“Post‑buckling behaviors of thin‑flm soft‑substrate bilayers with fnite‑thickness substrate”为题发表在SCI期刊《Scientific Reports》上,该期刊分级为中科院3区期刊,最新IF为4.379。
首先,研究人员将薄膜-软基体复合结构看作附着在弹性介质上的不可伸缩膜,并采用传统弹性空间法给出了基体的控制方程为
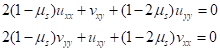
和
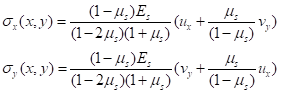
通过傅里叶空间变换,带入边界条件,得到了控制方程的解为
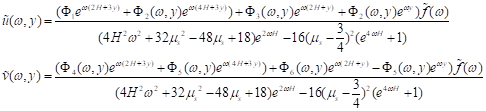
其中的系数函数
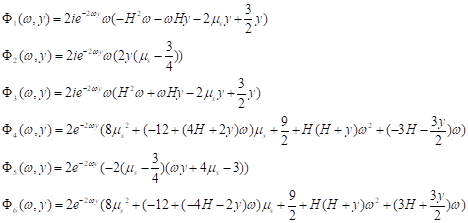
将基体对薄膜的作用求解出来后,耦合到薄膜的挠曲微分方程中,得到了有限厚度下的薄膜-软基双层结构的初始屈曲理论解。并将理论解与有限元分析结果对比如图3所示。
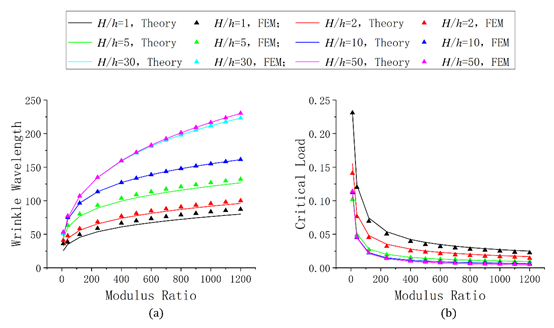
图3、不同膜厚比情况下,有限元及理论解计算得到的临界荷载与起皱波长
验证了有限元分析的正确性后,研究人员进一步进行了不同模量比和厚度比下的后屈曲模拟,并从中发现了4种新的屈曲路径,结合经典的屈曲路径,共分类总结为路径一至路径五如图4所示。
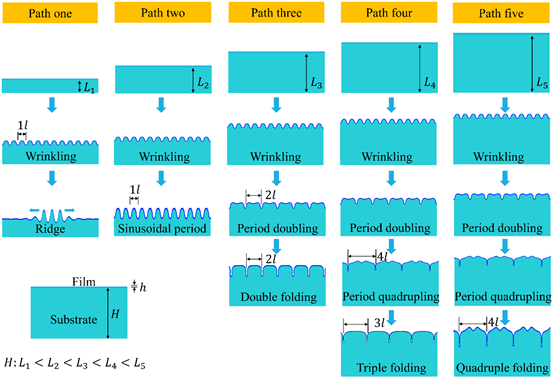
图4、路径一至路径五
其中,路径一在初始屈曲后,很快转变为局部隆起的情况,并在后续的荷载作用下,隆起的波峰逐渐向两边扩展,并重新形成正弦周期模式,如图5。
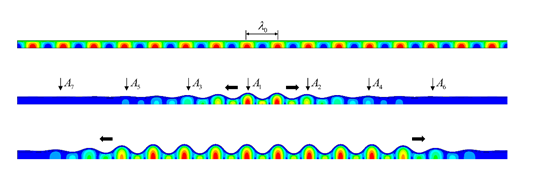
图5、膜厚比5,模量比600情况下有限元计算结果,其中薄膜在初始正弦周期屈曲后,很快坍缩成局部隆起的情况,并且这种隆起随着加载的进一步进行,隆起波峰向两边扩展,并最终重新形成正弦屈曲。
路线二和路线三的屈曲模式是逐步增大厚度比的结果,如图6和图7所示
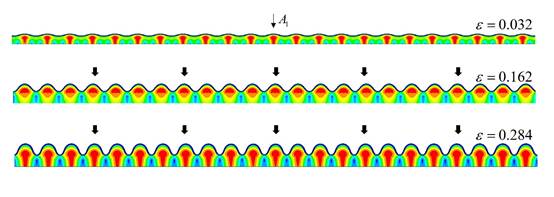
图6、模量比120情况下,厚度比10的有限元分析结果云图,其中薄膜在屈曲过程中只有单倍周期模式
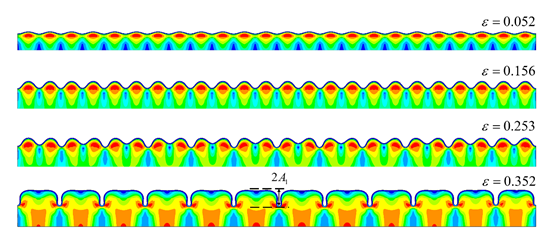
图7、模量比120、厚度比20情况下的有限元结果云图,其中薄膜表面经历了起皱-倍周期模式,并最终形成类似城墙形的双倍周期稳定形式
路径四与路径五综合反映了典型的无限大基体屈曲模式,不同的是,在考虑薄膜表面接触滑移作用后,路径四薄膜表面接触后,进一步荷载,会重新形成一个新的三倍周期的稳定模式,而路径五不存在这个过程,相关结果如图8和图所示。
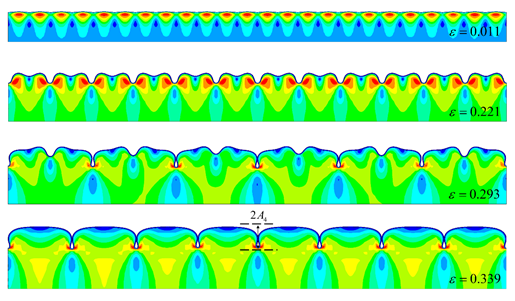
图8、路径四情况下的有限元模拟结果,在这个例子中,四倍周期的屈曲模态不是稳定的终点,薄膜表面的周期对称情况破缺后重新分布形成三倍周期的模式。
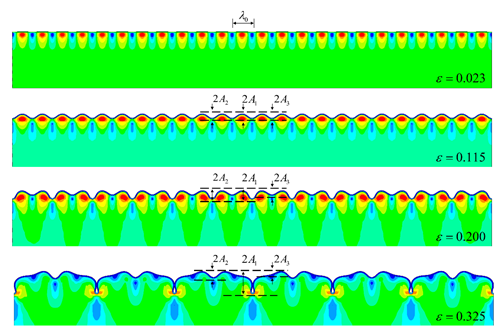
图9、模量比120、厚度比60情况下,有限元计算结果的等效应变云图,其中薄膜由初始屈曲后的正弦周期向双倍周期、四倍周期变化
最后,研究人员将所有的分析结果总结如图10所示。
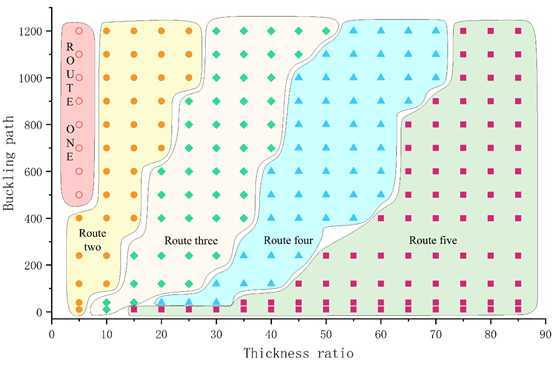
图10、不同模量比和厚度比情况下的有限元计算结果,其中的数据点代表不同的屈曲路径,每个区域中的结果从左向右以此为路径一至五。
有限元模拟效果
论文第一作者为博士研究生李蒙,通讯作者为孙博华教授。
文章链接:Li, M., Sun, B. Post-buckling behaviors of thin-film soft-substrate bilayers with finite-thickness substrate. Sci Rep 12, 4074 (2022). https://doi.org/10.1038/s41598-022-08136-w
该文由力学人公众号进行了报道:https://mp.weixin.qq.com/s/P1_COJelUpG7_jR9G7N_cQ
“有限厚度下的薄膜-软基双层结构后屈曲行为研究”—科研备忘录
2020级博士研究生 李蒙
2020年9月17日,孙老师在工作交流中,介绍了复旦大学徐凡教授团队的最新成果,双层膜结构的复杂屈曲形貌,这个简单的小结构在挤压荷载作用下,蕴含了丰富的屈曲变形结果,引起了大家的广泛兴趣,在了解到这个问题后,我立即向孙老师提议,采用有限元分析软件Ansys来尝试模拟一下这个问题,并深究下其中的科学问题。孙老师了解到后,对我的想法进行了鼓励,并建议我在复现原文的工作结果基础上,深入了解其背后的科学原理,并尝试考虑更多复杂的情况。
在后来一周的紧张模拟工作中,我初步复现了单倍周期模式,这个结果受到了孙老师的鼓励,孙老师建议我可以考虑更复杂的情况,如考虑基体的厚度、膜和基体的脱离、以及膜表面的接触问题等等。并可以将结果整理成论文,为学术贡献力量。
获得孙老师的指导后,我立刻进行了大量的模拟工作,然而问题的困难程度仍然超出了我的想象,薄膜和基体的后屈曲问题是一个高度非线性的问题,初始屈曲的单倍情况容易实现,但倍周期模式受到了各种因素的作用,这里,我的模拟结果一开始出现了极大的收敛困难,我尝试排除问题,并在之后的一个月时间内,反复尝试,但结果仍不理想。
这一个月时间我同时考虑了有限元模型的计算问题,和其他论文的过程进行对比后,我发现大家广泛都存在结果的不稳定性困难,这个问题在模拟上的最大困难应该是模型本身对边界条件的敏感性,传统做法是考虑叠加初始正弦缺陷后,再进一步进行屈曲和后屈曲分析。但我考虑到初始屈曲缺陷的叠加是否会对模拟结果本身有先入为主的影响,因而放弃了这个做法,转而寻找更好的思路。
我认为这个问题应该和边界条件有关,模拟的过程虽然有理论分析的支持,但模拟始终是一种数值计算的近似,这种分析方法在屈曲分叉路径上,拥有天然的计算敏感性,因而不合适的边界条件会放大计算误差,从而造成计算结果的不收敛,或者计算错误。因而,我在2020年10月中旬到12月份,始终尝试解决边界条件的设置问题,尝试了采用对称边界条件,但发现结果不成立,在反复尝试和调整之后,无奈放弃,(在后来的进一步学习中,了解到薄膜在屈曲成单倍周期或分叉成倍周期的过程中,往往存在对称性破缺,并重新形成对称性的过程,这个过程非常短,我后来通过提高荷载步数,大量计算后捕捉到了这种破缺并重分布过程,才揭开了问题的所在);也尝试了限制薄膜-软基两边竖向位移的方法,成功得到了单倍周期和倍周期的屈曲路径,值得注意的是,这一边界条件设置方法和清华大学教授冯西桥老师在其著作《材料表面失稳力学》中的有限元模拟方法的设置一致。然而冯老师只关注到了倍周期模式和无限大的基体情况下,在考虑有限大基体和更进一步的屈曲模式,这种边界条件由于限制了薄膜和基体两边的竖向变形,将不再能反映真实的变形过程,如图11所示。

图11、限制边界后,大荷载下的变形失真
问题的第一个重大解决发生在2021年1月份左右,此时我已经尝试了若干方法和思路,这时,我考虑到结合冯西桥老师的思路并解决荷载较大情况下的模型两边竖向变形情况,我尝试弱化了冯老师的边界设置,将竖向边界限制仅仅施加在薄膜两边,而基体两边放松,在控制底边竖向位移后,成功解决了更大荷载作用下的后屈曲模式,新的边界条件设置如图12所示。

图12、尝试的新的边界条件
通过这个边界条件的设置,我复现了基体厚度较大情况下的典型屈曲模式,在和孙老师交流后,孙老师表示认可,并鼓励我进行更多的模拟,然而,新的问题又相继出现,即是计算结果虽然形貌和典型屈曲路径一致,但屈曲波长和临界荷载和理论结果对比误差较大,我反应过来,这仍然是高度非线性带来的计算数值误差,即是虽然解决了收敛问题,但尚未解决精确问题。
下面的过程仍然是尝试解决这个问题,而解决方法很快出现,既在这个边界条件的设置下,只能采用细化网格数量,增加荷载步的方式,一步一步尝试提高收敛结果。而众所周知,有限元分析过程的细化和计算时间是一对矛盾的因素,期望精确的结果,那只有大幅度的增加计算时间。而提高计算速度又只能无奈的牺牲计算精度,通过测试对比,采用这个方案的模型,计算网格密度的设置要求非常惊人,如图13所示
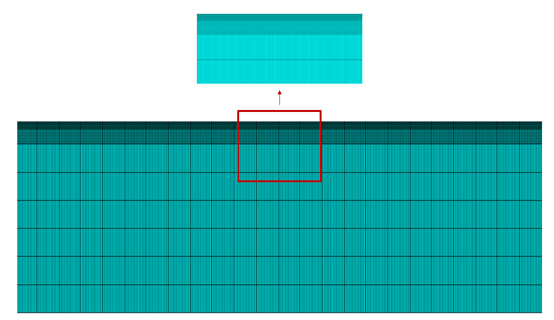
图13、设置的网格数量
同样困难的问题是计算荷载步的要求,由于采用这种弱化的边界条件,削弱了模型通过边界条件获得分叉的能力,而只能不停的通过增加荷载步,来给模型增加通过薄膜两边限制获得分叉的机会。经过初步尝试,要获得单倍周期,荷载步总数需要设置在1000步左右,计算一个完整的典型屈曲路径,采用先进的工作站,总计算时长也在3-5个小时左右,计算的速度实在让人无法接受。
此时,虽然获得了和理论结果一致的模拟结果,但牺牲了的计算时长限制了进一步探索的可能,考虑到要进一步计算薄膜表面接触和调整基体厚度的问题,这个模型仍然需要调整,而这个调整过程从2021年2月份直到2021年的7月份,中间参杂着进行实验的尝试和理论分析的尝试。
实验的努力和尝试在疫情的影响下举步维艰,最终无奈放弃;而理论的尝试却有了初步的进展,我在孙老师的建议下,通过学习基础理论知识和maple软件的应用,考虑将膜基双层结构等效成弹性地基梁的方法,采用弹性半空间法,通过傅里叶变换的方式,给出了初始屈曲情况下的理论解析,而对于后屈曲模式,我尝试采用摄动法去解决,然而,考虑厚度后的问题复杂度又一次超出了我的想象,摄动法二阶的计算结果已经超出计算机能处理的限度,当然对于问题的分析也没有帮助,这次考虑到问题已经有了初步的结果,只能止步于此。
然而模型的第二个重要解决出现了,通过再次调整边界条件的方法,我们尝试给模型两边增加刚性柱来施加荷载,刚性柱和薄膜与基体之间采用接触设置,接触摩擦力为0,模型如图14所示。
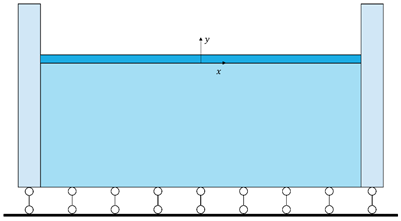
图14、更新后的模型结果
这样的设置成功加快了模型捕捉分叉的能力,从而能够设置更少的荷载步,并且更进一步的,通过给薄膜和刚性柱增加微小的摩擦力,并在初始屈曲后将摩擦力重新设置为0的情况下,可以更进一步的加快收敛速度,降低计算时间。通过测算,这一过程成功的将总荷载步数降低为100步左右,计算时间相比之前设置方式的3-5小时减少为十几分钟左右,效果非常显著。
最后,通过有限元分的分析,我考虑了有限厚度的情况,和薄膜表面接触滑移的情况,模拟结果却惊讶的发现,厚度的影响居然对后屈曲模式有显著的作用,原来认为的单一屈曲模式在这里,通过基体厚度的不同,重新整理分析成为了五种,即我们重新定义的路径一到路径五。
8月底,在中文稿定稿后,孙老师建议我进行英文翻译,将我们的学术成果向更广泛的科学同行们推广。于是接下来的一个月时间,我通过努力的写作,在9月底完成了论文的英文初稿。在尝试了若干期刊后,最终于2021年10月21日投稿至SCI期刊《Scientifc Reports》上,并在经历了焦急的等待过程中,于2022年1月17日获得了一审两位审稿人的审稿意见。
一审两位审稿人均同意接收,这个了我很大的鼓励,但也明确了需要我解决一些写作上的问题和解释澄清审稿人在阅读过程中的疑问。这里非常感谢两位尽职尽责的审稿人,两位审稿人共提出了21条审稿意见。此时虽然临近春节,但我仍然迅速的投入了紧张的修改工作中去,并针对审稿人的意见,丰富完善了论文中的阐述和说明,并且最重要的一点是其中一位审稿人指出了我对于一篇参考文献理解的错误,这篇来自锁志刚院士的文章在我初次阅读的时候,对于其中的一些内容理解不够深入,但是在这位审稿人的简单点拨下,我瞬间明白了之前理解不透彻的地方,也对这位素未蒙面的大师产生了敬佩之情。最后,怀着忐忑的心情,我提交了这次论文的修改稿,并满心期待接下来的返修意见。
这个过程中,孙老师对我的一审结果表达了祝贺,并及时地提醒我准备好论文的付款等工作,孙老师此时在2022年的前两个月左右也自己独立发表完成了两篇高质量的一区论文,他的工作成果震撼和激励了我们所有人。
最后在2022年3月2日晚,孙老师最先看到论文录取的信息,并欣喜的在工作交流群中祝贺了我。看到这个消息后,这一刻我感到了无比的开心和欢乐,此时,再次回想起之前的种种努力和尝试,以及和孙老师讨论交流的过程,以及其他同学们的鼓励。回忆起熬夜看模拟结果,在图书馆翻阅屈曲文献资料,第一次尝试使用maple软件,并从头学习的过程。只是这个过程中有70%都是不停的失败和挫折,但也有瞬间的成功解决了之前的种种困境。后来我不止一次的思考过,当时要是没有坚持努力寻找更合适的边界条件,没有花费大力气来尝试降低计算时间,从而使得更进一步的考虑表面接触滑移、考虑有限厚度成为可能,那我也不可能完成这篇文章,更加遗憾的是将不可能看到从路径一到路径五这五种新颖的、多彩纷呈的屈曲路径和屈曲形态。
最后,孙老师一次次的强调了“科研十条”,这里再次提醒并勉励自己。
1、加强基础理论修养公式一定要自己推导,边干边学要带着问题学习及时弥补自己知识结构;
2、从第一原理出发要设想如果问题是你第一个研究应当怎么做;
3、思路开阔要有不同维度和层次的联想思维;
4、目光高远要敢于越过历代权威的工作努力创新;
5、要有的放肆抓大放小抓主要放次要集中力量解决要害的问题;
6、要追根求源尽力了解课题的发展历史;
7、要尽量多掌握科研需要的各种工具包括软件使用和实验设备使用;
8、要按照课题本身的逻辑发展不断提出新问题把研究推向前进;
9、每项研究都要有理论、数值模拟和实验的相互验证并及时总结写成论文发表;
10、要时时刻刻思考如何把科研成果形成核心技术转化成专利并设想可能的应用场景。