孙博华教授团队:圆环壳和椭圆环壳结构非线性Gol'denveizer问题研究

环壳结构由于其几何构型,具有特别的力学性能。在众多的环壳结构问题当中,其中有一个非常有趣的问题,叫做Gol'denveizer问题。最早的Gol'denveizer问题可以描述为:考虑一个环壳结构,采用圆柱面aa将环壳结构切割成两部分:A和B;A为正高斯曲率部分,B为负高斯曲率部分。假设分别在A、B部分施加一个外部的表面载荷,如图1所示。从整体上考虑,该结构在该荷载作用下是静态平衡的,但是分别对A和B部分进行分析发现,结构的每个部分竖向轴均会有一个分力。正如我们从壳体膜理论中知道的那样,环壳结构是弹性的,也就是说,环壳结构没有发生非常小的弯曲。当环壳结构发生刚体位移时,外荷载是自平衡的,环壳结构发生刚体位移时并不做功。然而,我们可以很容易地证明,环壳结构在受到这样荷载作用下,膜应力状态是不可能的。这是因为当我们移除B部分,并由施加在A部分上的膜力沿着这两个轴线方向进行分解;结构的平衡状态就会被打破。所以采用壳体膜理论并不能很好来描述这个状态下的环壳结构。
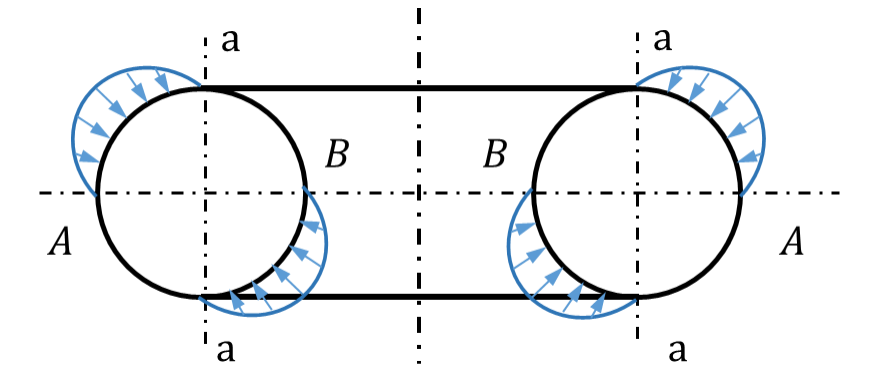
图1 Gol'denveizer问题的描述
这一问题在提出后并没有引起众多学者的关注。直到2002年,Audoly和Pomeau通过只考虑竖向力的方法简化了该问题,如图2所示。随后,Audoly和Pomea利用环壳结构的膜理论并且结合非线性边界层扰动理论对环壳结构的Gol'denveizer问题进行了详细的研究,并且得到了环壳结构Gol'denveizer问题的近似解,并给出了合力F和竖向位移的简单公式:
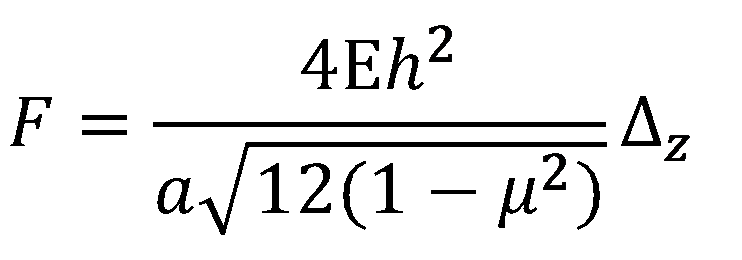
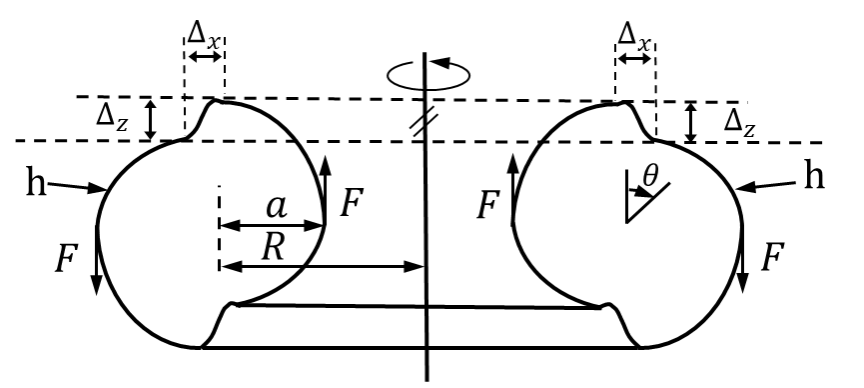
图2 Gol'denveizer问题的变形图
虽然Audoly和Pomeau得到了环壳结构的Gol'denveizer问题的解析解,但是这个解得真实性和准确性并未得到证实。在2022年,孙博华院士利用壳体结构的弯曲理论求解了Gol'denveizer问题,发现了采用壳体结构的膜理论对环壳结构Gol'denveizer问题进行计算会导致奇异解的出现,并且证实了环壳结构的弯曲理论可以得到环壳结构Gol'denveizer问题的完整解。此外,孙博华院士还证实了Audoly和Pomeau采用膜理论并且结合非线性边界层扰动理论得到的近似解析解具有极高的准确度。
至此,环壳结构的线性Gol'denveizer问题均已经研究完毕。但是对于环壳结构的非线性Gol'denveizer问题还并未有人涉猎。于是,在这些前人的基础上,我们采用非线性有限元分析的方法分别对圆形环壳结构、椭圆形环壳结构的非线性Gol'denveizer问题进行研究。
首先我们采用有限元软件ABAQUS分别对圆形环壳结构和椭圆形环壳结构非线性Gol'denveizer问题的位移进行研究,得到相对应的位移-转角曲线。具体的位移-转角如下图所示。

圆形和椭圆形环壳结构的竖向位移曲线
随即我们得出其相应的位移云图:
圆形和椭圆形环壳结构的竖向位移云图
除此之外,我们还得到圆形环壳结构和椭圆形环壳结构非线性Gol'denveizer问题相应的力-转角曲线和云图,
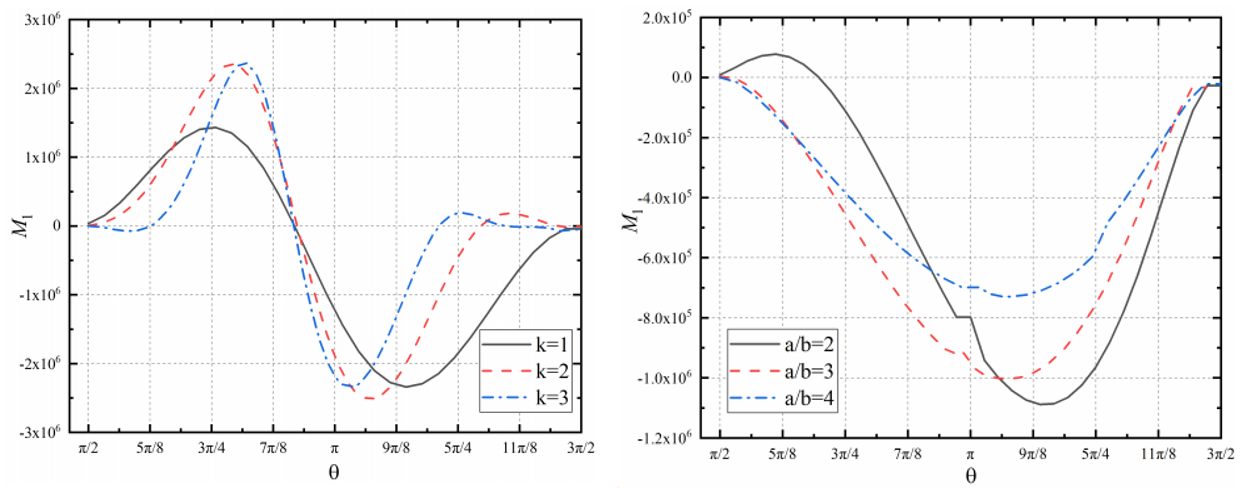
圆形和椭圆形环壳结构的弯矩曲线图
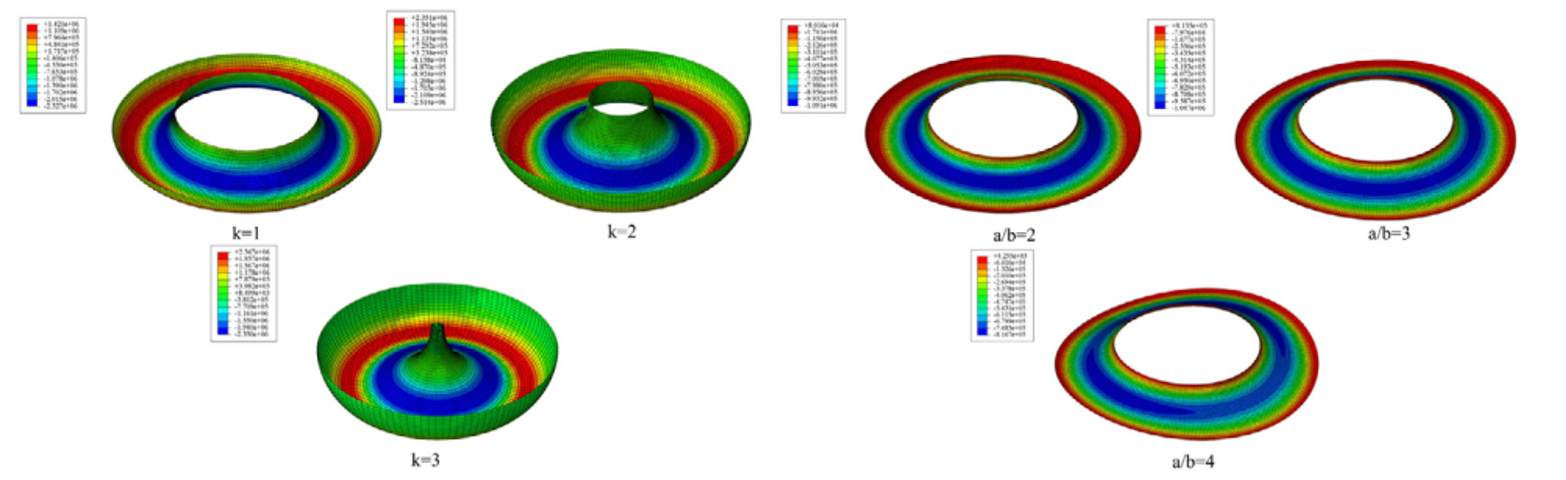
圆形和椭圆形环壳结构的弯矩云图
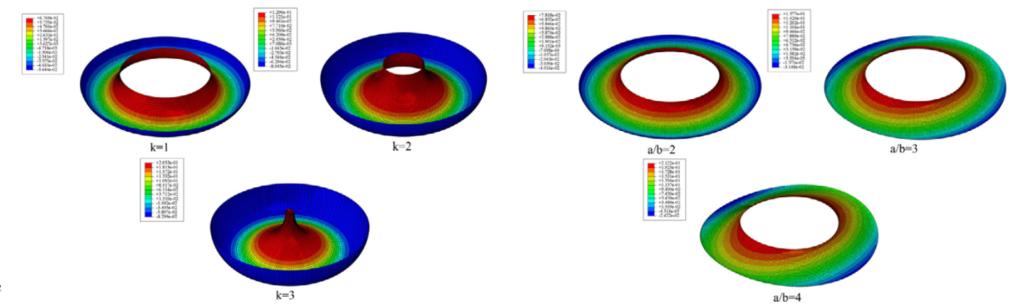
此外,我们又对环壳结构的Gol'denveizer问题的屈曲性能进行研究,分析发现随着半径a的增加,圆形环壳结构具有更丰富的屈曲现象。椭圆环壳结构在受到竖向相对荷载的作用下会出现一种类似于裙褶的屈曲现象。并且随着半径比a / b的增大,椭圆环壳结构Gol'denveizer问题的屈曲荷载逐渐增大。不同类型环壳结构Gol'denveizer问题的屈曲曲线与破坏模式图如下图所示。
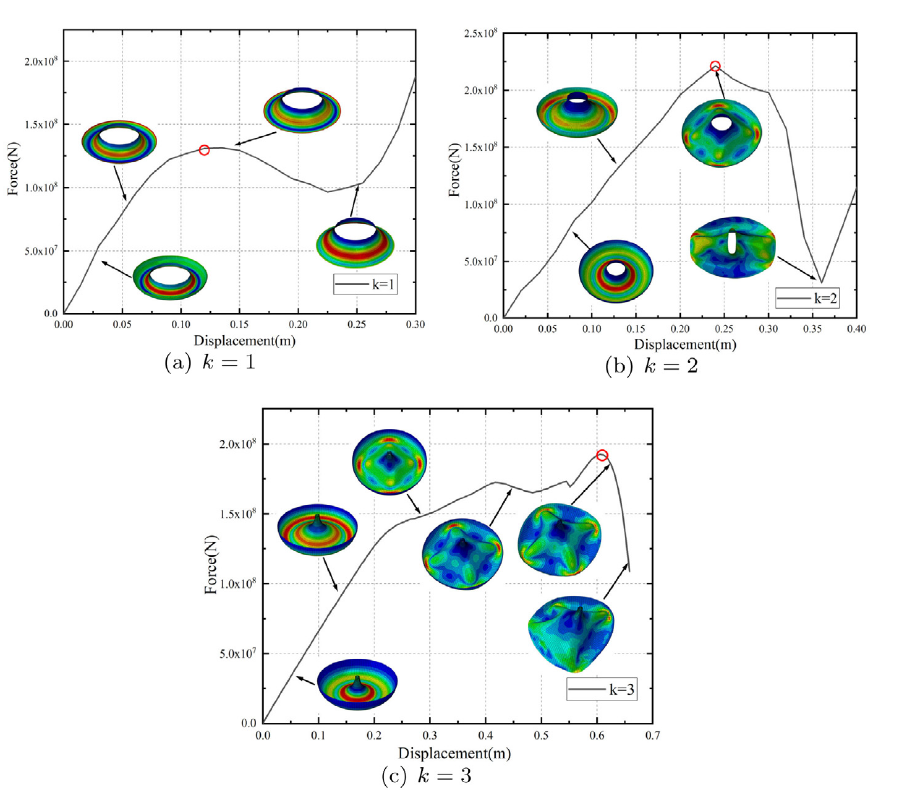
圆形环壳结构的屈曲破坏模式图
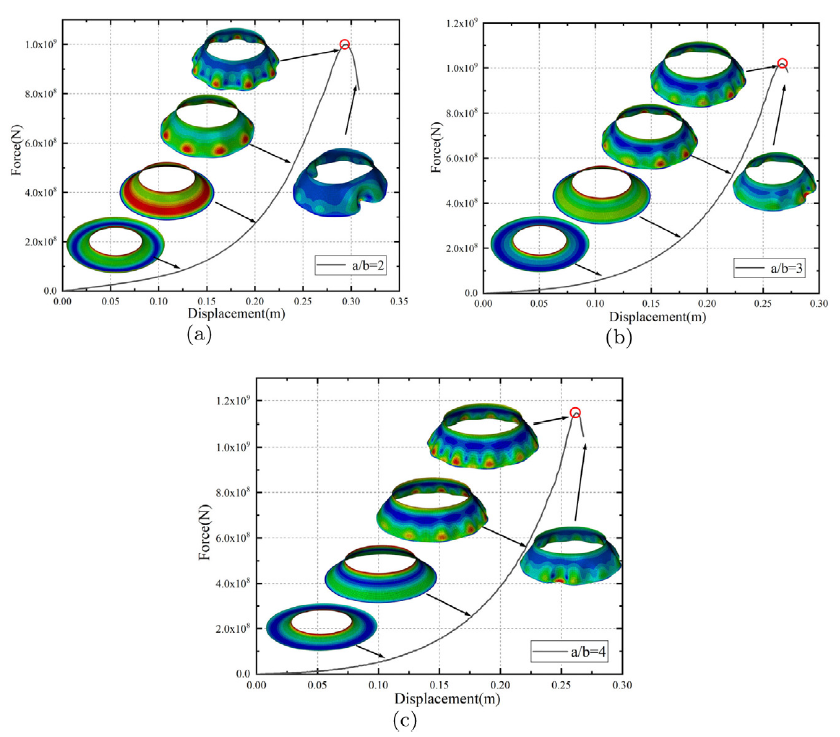
椭圆形环壳结构的屈曲破坏模式图
这篇论文以西安建筑科技大学土木工程学院为第一完成单位,第一作者为2019级博士研究生宋广凯,通讯作者为孙博华院士。《Thin-Wall Structure》2021-2022年影响因子为5.881,中科院分区二区期刊。
文章链接:Guang-Kai Song, Bo-Hua Sun, Nonlinear investigation of Gol’denveizer’s problem of a circular and elliptic elastic torus, Thin-Walled Structures. 180, 109862 (2022). https://doi.org/10.1016/j.tws.2022.109862
“环壳结构非线性Gol'denveizer问题研究”
研究生科研备忘录
2019级博士研究生 宋广凯
本人在研究生阶段第二篇英文学术论文定稿后,为了更好的复盘这个令人难忘的科研过程,在此特写学术备忘录,详细地记录此次科研的过程:
在2020年寒假,孙老师撰写了环壳结构Gol'denveizer问题相关的文章,文章中采用了壳体弯曲理论对环壳结构Gol'denveizer问题进行研究。孙老师建议我使用有限元软件ABAQUS对线性环壳结构的Gol'denveizer问题进行模拟,并得到其位移-转角,力-转角曲线与理论进行对比。在刚刚收到这一任务的时候我是既开心又紧张,开心是因为可以借此机会锻炼一下自己的有限元能力,紧张是因为害怕自己无法将该问题模拟出来。怀着这种忐忑的心情,我开始了使用有限元软件ABAQUS对线性环壳结构的Gol'denveizer问题进行模拟。
一开始的模拟并不是特别顺利,有限元计算出了来的环壳结构Gol'denveizer问题的位移和力的数值均偏大,这使得我有些迷茫。于是我又对老师的文章进行更深层次的阅读,在对老师的论文进行进一步的研读时发现,由于我的粗心大意把施加在环壳结构上的合力作为均布力施加到了环壳结构上。正是因为这一原因导致的模拟结果偏大。针对这一问题,我及时做了修改并将得到的有限元结果发给老师与理论结果进行对比。通过对比发现有限元结果与老师的理论结果非常吻合,这给了我莫大的信心。
开了学以后,由于需要进行风洞项目,由于我只关注于项目的进度并未再对环壳结构Gol'denveizer问题进行更进一步的研究,环壳结构的Gol'denveizer问题就被搁置了。在一次会议上孙老师告诫我,不要因为现在的风洞项目影响了自己原本的科研进度,要一手抓科研,一手抓项目。并且孙老师还建议我可以对环壳结构的非线性Gol'denveizer问题进行研究并写成文章。于是我在之前线性模拟的基础上开始了环壳结构Gol'denveizer问题的非线性模拟。并且在模拟过程中,孙老师提醒我可以把椭圆形环壳结构一并进行研究,并且在分析一下圆形环壳结构和椭圆形环壳结构的屈曲特性。这一建议瞬间打开了我的思路,我茅塞顿开,随即便开始着手对椭圆环壳结构非线性Gol'denveizer问题进行模拟,并且在有限元中尝试研究圆形环壳和椭圆环壳结构的屈曲特性。
两个月之后,所有的模拟已经进行完毕,我便开始了文章的撰写。由于这是第二篇英文文章,我萌生出了一个想法,是否可以尝试不写中文稿,直接用英文撰写文章。为此我阅读了许多文章,并且将其中的语言、词汇等记录下来方便以后英文稿的撰写。在准备工作完成之后我便开始了英文稿的撰写。两个月之后,我已经完成了英文稿件的撰写。在2022年12月我将最终的英文稿发给孙老师,孙老师在阅读完文章之后便邀请我去他家进行讨论。在老师家中,孙老师明确指出我的英语能力不够,逻辑思维不清晰,不能够直接采用英文撰写文章,还是要先写成中文稿再进行翻译。并且文章中还存在些问题。孙老师把问题逐条给我说清楚,并且告诉我如何修改。那一天我与孙老师讨论到了很晚,孙老师对我文章的撰写、研究提出了非常宝贵的意见,也正是因为孙老师一丝不苟的科研态度,才有之后文章的顺利录用。
在经过了近一个月的修改,文章的英文稿已经修改完毕。由于本人的英语水平太差,孙老师建议我将最终稿件提交润色。一开始我投稿的期刊是《Journal of the Mechanics and Physics of Solids》很快便被编辑退稿。之后,孙老师给我发消息建议我投稿《Thin-Walled Structures》。在2022年1月2号,我将该文章投稿到《Thin-Walled Structures》期刊上。现在回想起来,正是因为这一建议,使得我少走了好些弯路,文章能顺利发表离不开孙老师对期刊的选择。
在投完稿件之后便是焦急的等待过程。终于在2022年4月25号下午六点,孙老师通知我现在过来讨论审稿意见的论文修改。我怀着忐忑的心情来到了老师家楼下,和老师在楼下花园中促膝长谈。老师说,这篇论文有这样的审稿意见是最好的结果,并将邮件转发给我。通过阅读邮件发现,稿件一审有三个审稿人,后两个审稿人的意见均是修改后录用。随后孙老师询问我是否对环壳结构的Gol'denveizer问题有着深刻的理解,让我自己把Gol'denveizer问题描述一下。然而我对Gol'denveizer问题描述并不深刻,自己的回答也是不尽人意。孙老师又苦口婆心的给我讲解了Gol'denveizer问题的研究历史。老师详细的介绍让我茅塞顿开,并且孙老师告诫我,做学术要知之为知之,不知为不知,不能不懂装懂,对一个问题充分的理解是能够把这个问题以故事的形式讲出来。并且,在阅读完审稿人的意见发现,有两位审稿人写道:“本文章是在前人的基础上进行研究,是之前课题的延续”。由此可以看出,老师先前的研究无疑为我的文章奠定了坚实的基础。文章后来的顺利接受于老师先前的工作密不可分。
在与老师沟通交流之后,我怀着紧张的心情根据审稿意见,开始了对文章的修改。在我改完论文之后,孙老师又对我的摘要部分进行了修改,并且告诫我中文文章的撰写一定要逻辑清晰,这样翻译成的英文文章读起来才会更加通顺。为了增加文章被录用的概率。孙老师建议把修改后的文章拿去再润色一遍。在所有修改工作、文章润色完成之后,我提交了这次论文的修改稿,并满心期待接下来的返修意见。
最后在2022年7月19日晚,孙老师最先看到论文录取的信息,并高兴的在工作交流群中祝贺了我。看到这个消息后,这一刻我感到了无比的开心。此时,再次回想起之前的模拟,论文写作以及和孙老师讨论交流的过程。点点滴滴中无不包含着孙老师的关心。回顾这次科研的整个过程,我迷茫过、气馁过、难过过,但每一次解决困难后的开心让我终身难忘。这篇英文论文的完成,不仅是科研能力的提高,更是内心的成长。我要感谢孙老师在此论文的选题、构思和撰写等方面给予的指导与帮助。在这次论文写作过程中出现的错误、问题等我会铭记于心。认真总结并反思之前的不足,全力以赴的奔向更高的学术山峰。
在论文正式发表了之后,孙老师建议我对该研究成果写一篇报道。于是我就对该研究内容进行了整合和写作。当我将报道发给孙老师之后,老师告诉我要跳出论文写作思路,总结文章的精华,并且孙老师又对我的报道进行了较大的修改。孙老师从环壳结构研究的起源开始,高屋建瓴介绍了国内外环壳结构的研究历史,我读后大为震撼,因为只有非常大的格局和非常高的大局观和历史观才可以将环壳结构的研究历史讲述得如此清晰。并且孙老师将该报道投搞到了力学人公众号,在9月19号获得了正式推送。此外,在9月22号西安建筑科技大学笃实新闻网也对本成果进行相关的报道。在这几次的报道写作当中,孙老师对环壳问题的来龙去脉的介绍,让我对环壳结构的研究历史有了更深层次的理解,并且让我明白对一个课题的研究要站在更高的层次上,要时刻保持一种大局观,将该课题的研究历史清晰地以故事的形式讲出来,才是对这个问题的真正的理解。
以上内容均为本人此次科研经历的真实记录,包含了我从文章的开始到文章录用的全部内容,希望研究院同学可以加以借鉴,少走弯路,多出成果。最后,孙老师一次次的强调了“科研十条”,这里再次提醒并勉励自己。
1、加强基础理论修养公式一定要自己推导,边干边学要带着问题学习及时弥补自己知识结构;
2、从第一原理出发要设想如果问题是你第一个研究应当怎么做;
3、思路开阔要有不同维度和层次的联想思维;
4、目光高远要敢于越过历代权威的工作努力创新;
5、要有的放肆抓大放小抓主要放次要集中力量解决要害的问题;
6、要追根求源尽力了解课题的发展历史;
7、要尽量多掌握科研需要的各种工具包括软件使用和实验设备使用;
8、要按照课题本身的逻辑发展不断提出新问题把研究推向前进;
9、每项研究都要有理论、数值模拟和实验的相互验证并及时总结写成论文发表;
10、要时时刻刻思考如何把科研成果形成核心技术转化成专利并设想可能的应用场景。
媒体报道:
力学人:
西安建大孙博华教授团队:关于圆环壳和斜椭圆环壳结构力学问题:https://mp.weixin.qq.com/s/6naX7myJT-WSRUuTT0fW-Q
笃实新闻网:
西安建大孙博华院士团队:关于圆环壳和斜椭圆环壳结构力学问题的系列https://www.nature.com/articles/nphys4225