薄壳结构几何上看上去是一种平面结构经过弯曲而成的结果,由于其优越的力学性能和优美的空间造型,被广泛的应用于建筑和工业领域。例如,拱桥和教堂穹顶等。

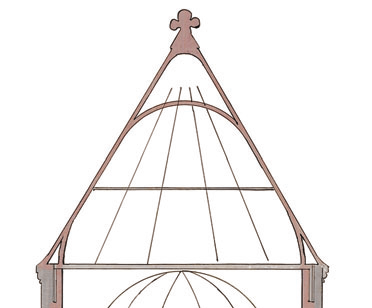

由于壳体形状直接影响其承载能力,所以寻找比较优化的形状就成为壳体力学的难题之一。一般而言,受压壳体的最优形状是在给定荷载和边界条件的情况下其横截面上的弯矩越小越好时对应的形状,换句话说,壳体最好是处于无矩状态。这样的壳体横截面上只承受压力而没有弯矩。
英国科学家胡克(Robert Hooke)于1676年发表了10个“Inventions”(发明),其中第三个发明就是材料力学中著名的胡克定律,而第二个发明描述了“the true Mathematical and Mechanical form of all manner of arches for building”:

胡克这个发明的基本思想是利用自重作用下的悬链线形状,作为受压的拱形,从而使拱横截面上的弯矩为零,这样的拱称为“Catenary Arch”(悬链线拱)。
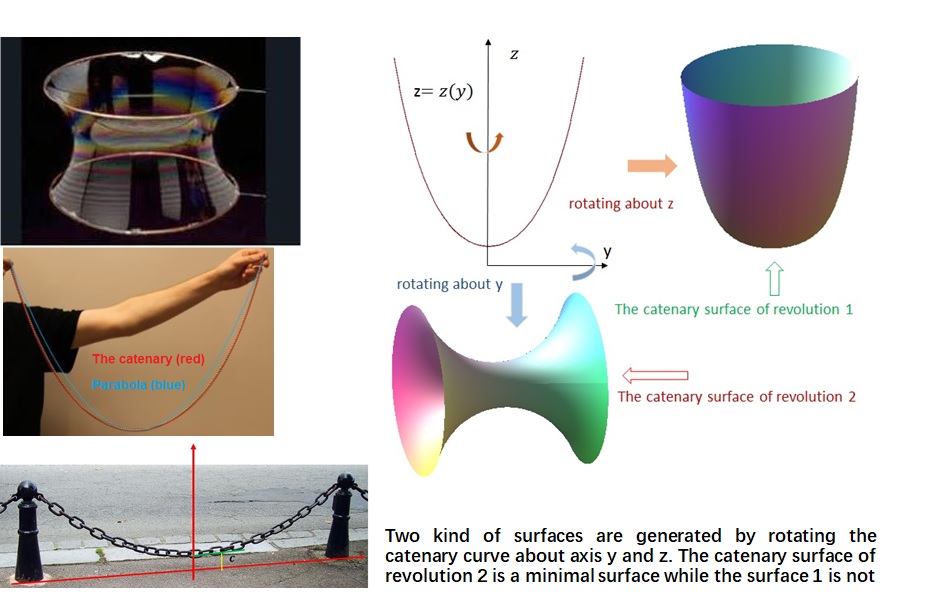
悬链线旋转一周可以生成一系列曲面,其中的一个曲面的面积最小,即悬链线面“Catenoid”。这种最小面的平均高斯曲率为零。这个最小面问题也是变分方法一个非常著名的例子,即求通过二固定点的一条曲线旋转生成曲面的最小面积问题。
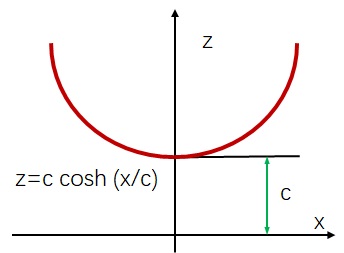
悬链线壳体作为一种有悠久应用历史的壳体结构,可惜的是找不到有关其变形和应力分析的文献,唯一的理论结果是苏联著名力学家 V. V. Novozhilov 在其《薄壳理论》的简单讨论,有关数值结果根本就找不到。为了弥补关于悬链线壳体研究的不足,孙博华教授利用旋转薄壳的位移型和混合型二种方程组详细研究了悬链线壳体的变形和应力问题,为了更好地理解悬链线旋转壳体的变形和应力,孙博华教授推导了二种悬链线旋转壳体的主曲率半径,以及悬链线旋转壳体位移型控制方程。孙博华教授对于悬链线旋转壳体的这个位移型方程和Reissner-Meissner混合型方程进行了数值计算和对比。计算显示悬链线旋转壳体的力学性能对于悬链线几何参量 c 非常敏感,揭示了对于一些荷载情况悬链线旋转壳体的力学性能优于相应的球壳。论文还提供了二个完整的 Maple 程序。研究结果:B. -H. Sun,Small symmetrical deformation and stress analysis of catenary shells of revolution,Acta Mechanica Sinica,38,421425(2022).已经在线发表,孙博华教授为唯一作者。
作者孙博华教授,江苏徐州人,2010年当选南非科学院院士,现任西安建筑科技大学力学技术研究院(IMT)院长、首席科学家、土木工程学院教授、博士生导师。主要从事连续介质力学、细薄结构、智能复合结构,仿生结构力学、湍流、力学问题标度律等方面的研究。曾主持过多项南非科技部和南非国家基金会的研究课题多项,发表学术论文百余篇,编著出版专著多部。兼任中国力学学会第十一届理事会特邀理事、《Acta Mechanica Sinica》编委、《力学进展》第六届编委会特邀编委。曾任南非开普半岛技术大学教授、大学Senate和Centre for Mechanics and Technology主任、暨南大学国际学院首任院长和理工学院一级特聘教授、北京大学工学院访问教授、曾获2017年度清华大学杰出博士后校友奖。
课题组招收力学博士和博士后(仿生结构力学、细薄柔性结构力学、流固耦合、流体力学方向),热情欢迎青年才俊与我们联系。邮箱:imt@xauat.edu.cn,网址:http://imt.xauat.edu.cn。
原文链接:
https://www.sciengine.com/publisher/CSPM/journal/AMS/38/1/10.1007/s10409-021-09055-t?slug=fulltext