孙博华教授:Navier-Stokes方程的一种等价形式

粘性流体力学的Navier-Stokes方程:

Navier-Stokes方程的求解是数学上的一个难题,其根源是因为(convective term)对流项(v·▽v)的存在。从张量分析的角度,对流项(v·▽v)其实是流体速度梯度与流体速度的标量积,是速度梯度对速度的变换。由于这一耦合项的存在,导致了Navier-Stokes方程具有强烈的非线性。
不过,这个对流项的存在也有个优点,就是可以使我们可以通过流体速度梯度的逆张量((▽v)-1),把其中的流体速度分出来(至少是从形式上),从而可以获得一个流体速度的形式解:
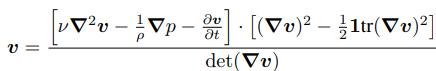
这样分解出来的流体速度非常自然的提供了一种新的迭代求解的结构:

这个迭代结构的优点是只有微分运算,希望有助于CFD以此开发出新的算法。
研究结果已经Online发表: B.H. Sun, An equivalent form of the Navier-Stokes equations, Acta Mech. Sin., Vol. 39, 322241 (2023)
论文连接:https://www.sciengine.com/AMS/doi/10.1007/s10409-022-22241-x;JSESSIONID=5e44c474-e739-4497-8e85-1a09a21bfe45