
2021年3月22日,我的师兄,清华大学的任文敏教授写信给我,问我有没有关于悬链线旋转壳的相关研究,有趣的是,我已经为这个问题研究了一段时间。
旋转曲面是通过绕轴旋转二维曲线而产生的曲面。因此,所产生的表面总是围绕轴具有方位角对称性。其中,即当二维曲线为悬链线时存在一个最小的表面积。悬链线是使悬浮均匀柔性链的势能最小的形状。通过将悬链线曲线分别绕y轴和z轴旋转,可以生成两种曲面,(图1),其中表面2是一个最小的旋转表面。
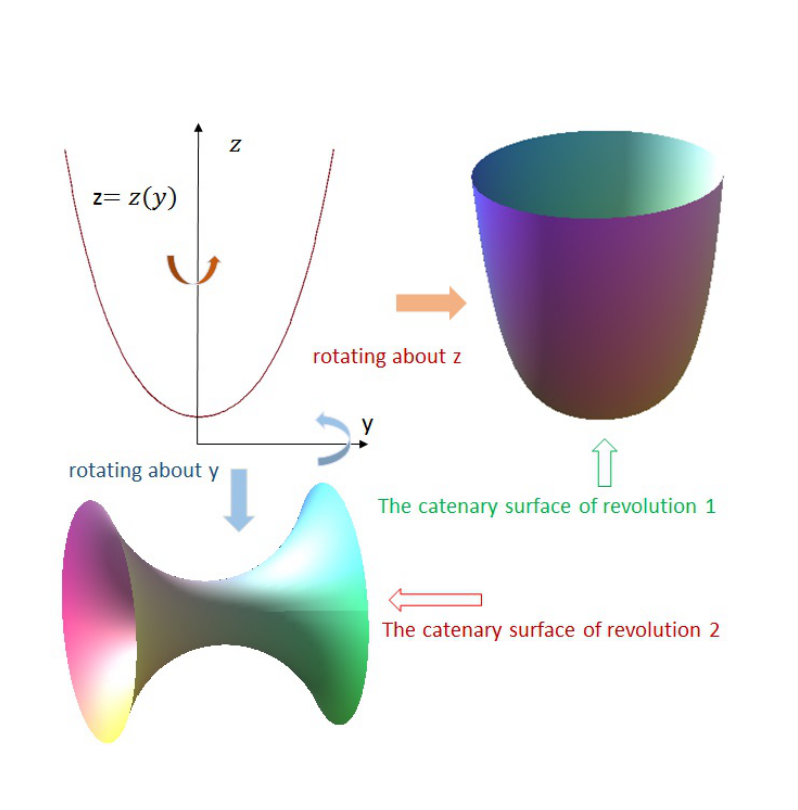
图1 悬链线旋转壳体的几何图形
虽然壳结构以旋转面作为中间表面广泛应用于教堂建筑,但作者没有找到任何的科学出版物对悬链线旋转壳体的分析。为了填补该方面的空白,我们利用壳体的弯曲理论研究了其应力、应变行为。为验证本文工作的准确性,我们将悬链线壳体的位移型控制方程的结果与Reissner-Meissner混合型控制方程的结果进行了对比验证(图2)。
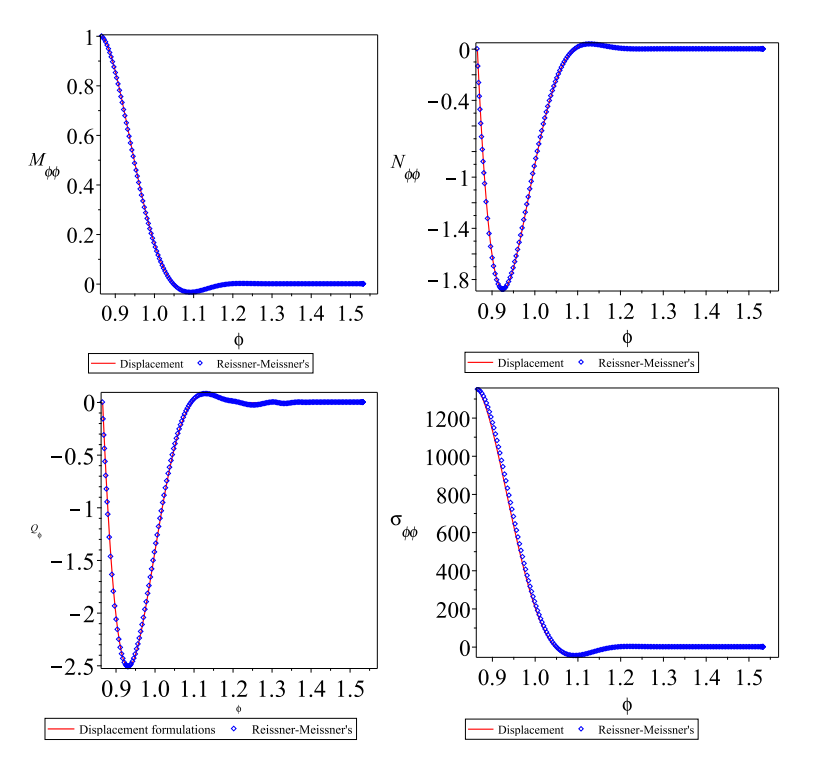
图2 结果对比验证
最后,将悬链线旋转壳体与球壳进行对比发现,悬链线旋转壳体最大应力和变形区域比相应的球壳小得多,除一些边界效应外,几乎处于薄膜应力状态。同时,在过载条件下,悬链线旋转壳的力学设计优于球壳(图3)。
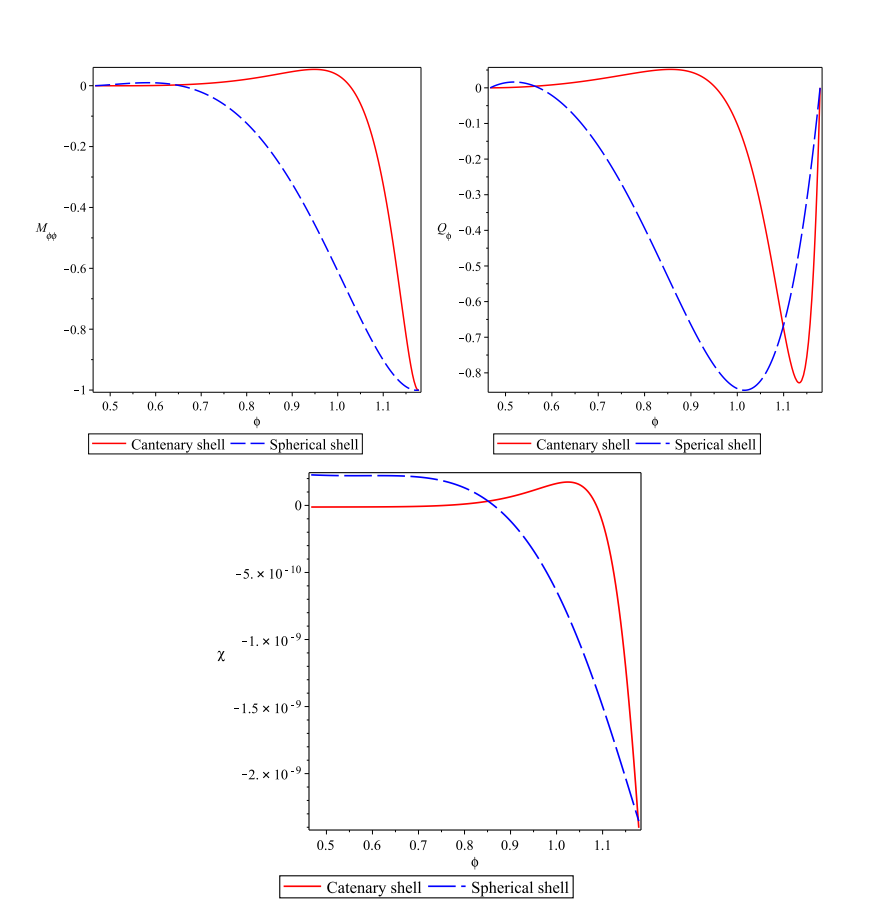
图3 悬链线旋转壳与球壳应力、位移响应对比
《Acta Mechanica Sinica》2021年影响因子为1.975,中科院分区3区期刊。这篇论文以西安建筑科技大学为第一完成单位,孙博华院士为论文唯一作者。
文章链接:B.H Sun,Small Symmetrical Deformation and Stress Analysis of Catenary Shells of Revolution,Acta Mechanica Sinica. (accepted)