
拿一张纸条,抓住两端,使之形成弧形,当两端同时往里旋转时,纸条首先会偏转,然后后退,最后会快速翻转以返回到其先前的形状(图1)。扭转驱动下拱形薄带的形态转换问题是一个与日常生活相关的科学问题,拱形薄带可以通过能量转换在很短时间内达到很高的速度,然后再恢复到结构的原始形状。这类结构可以实现周期性的快速运动,而不需要额外的恢复过程,对于很多设计而言,这是一个明显的优势。
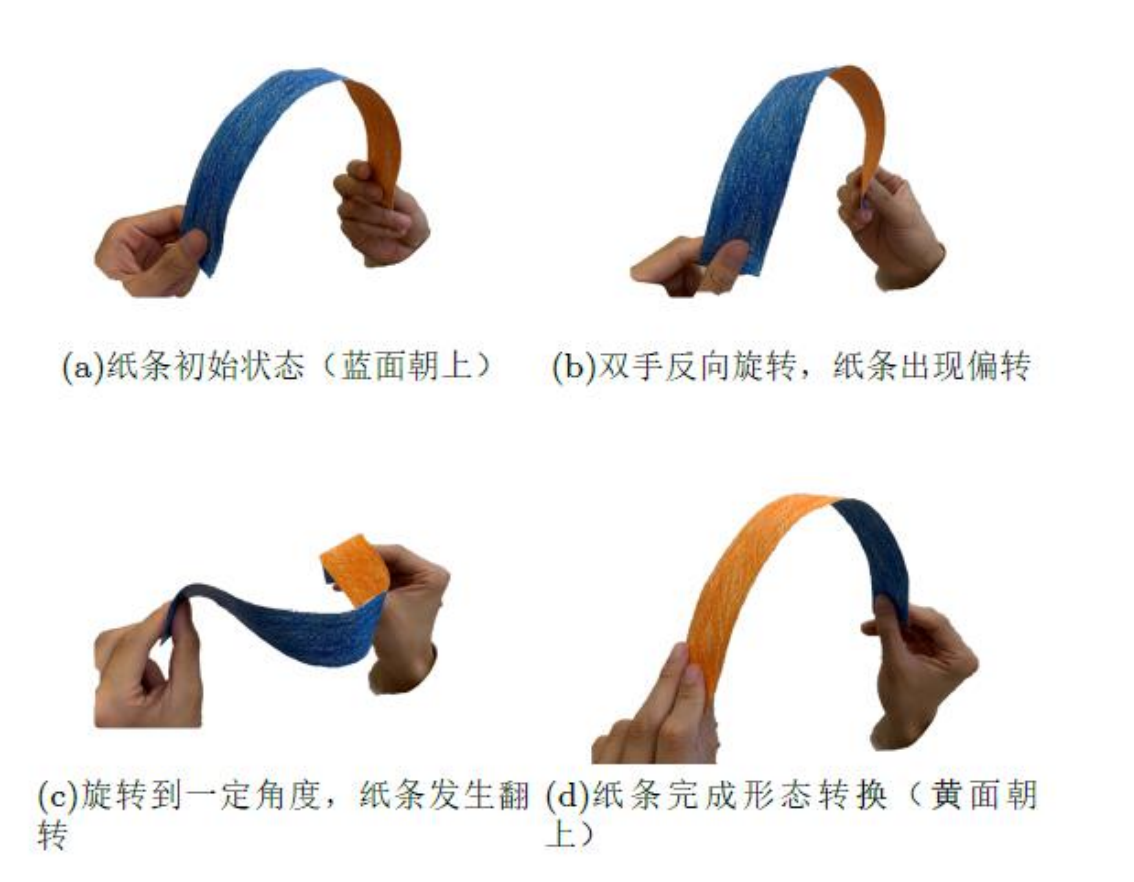
图1:纸条的形态转换过程
在此基础上,西安建筑科技大学力学技术研究院孙博华院士团队开展了对扭转驱动下拱形薄带形态转换的研究,我们的结果对于理解和设计这种拱形薄带的结构具有指导意义,且可以适用于不同规模的问题。相关工作于2021年以“Morphological transformation of arched ribbon driven by torsion”为题发表在SCI期刊《Thin-Walled Structures》170 (2022) 108511上,《Thin-Walled Structures》分级为中科院2区期刊,并入选建筑科学领域期刊分级T1。审稿人对此文章给与了积极评价:
“The authors established a mathematical model of the arched ribbon dynamics driven by torsion by using Kirchhoff rod equation. They simplified the elastic deformation energy of the ribbon model derived by Sano and Wada to show the variations of the Euler angle of each point on the center line of the ribbon. They also used ABAQUS, a commercial finite element package, to simulate the problem and compared the results between simulation, theory and experiments conducted by Sano and Wada. They further showed that the ratio of the in-plane stretch elasticity and Kirchhoff strain energy is affected by the length and thickness ratio, and used dimensional analysis theory to establish the critical width formula with different cross section. I think this part has important significance for designing arched ribbons driven by torsion.”
首先,研究人员根据薄带结构的特点,从Kirchhoff杆方程出发建立了扭转驱动下拱形薄带结构动力学的数学模型,并推出了薄带中心线上各点的欧拉角随弧坐标s和支座转角Ø的变化规律:

同时,我们还计算了不同泊松比对该结构的影响(图2)。
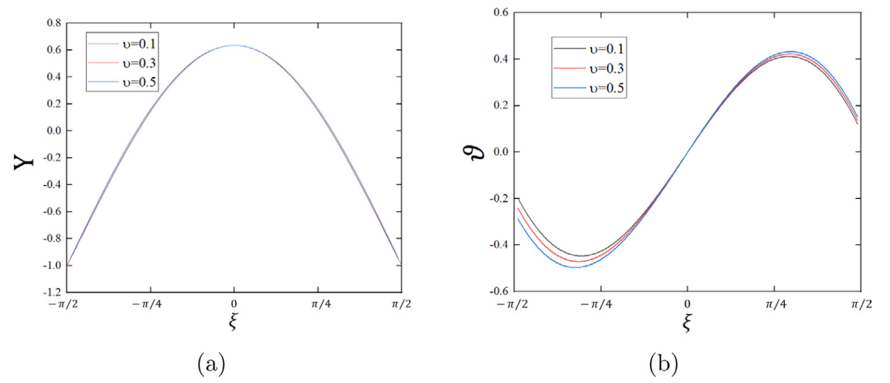
 图2:不同泊松比对结构的影响
图2:不同泊松比对结构的影响
随后,我们运用非线性有限元分析工具来模拟薄带的形态转换现象,在验证了理论模型后,我们进一步探讨了不同截面的薄带在“翻转flip”和“折叠fold”时临界宽度的变化,并在其中引入量纲分析的思想,最后,给出了临界宽度的一般公式:
 ,对于矩形截面,𝐴取3.19;对于椭圆形截面,𝐴取3.06。
,对于矩形截面,𝐴取3.19;对于椭圆形截面,𝐴取3.06。

图3:不同截面的“翻转”临界宽度问题
最后,研究人员还发现对于该拱形薄带结构,薄带的曲率半径与宽度两因素和薄带面外方向位移以及面外位移相对于扭转角度的变化率成正比(图4),即曲率半径和宽度一定范围内的增加会导致该结构可以储存更多的弹性势能,且转化为动能的速度更快;同时宽度的增加还会使“翻转”到来的时刻提前,而薄带厚度对“翻转”时间和位移变化率几乎没有影响。

图4:薄带宽度对结构的影响
论文第一作者为2019级硕士研究生戴远帆,第二作者为2019级硕士研究生张一,第三作者为2019级硕士研究生李翔,通讯作者为孙博华院士。
文章链接:Y.F. Dai, B.H. Sun, Y. Zhang, X. Li, Morphological transformation of arched ribbon driven by torsion, Thin-Walled Structures 170 (2022) 108511,https://doi.org/10.1016/j.tws.2021.108511
“拱形薄带在扭转驱动下的形态转换问题”备忘录
2019级硕士研究生 戴远帆
本人在研究生第一篇学术论文定稿后,在孙老师的建议下,特写此学术备忘录,详细地记录此次科研的过程:
2020年是不平凡的一年,由于疫情,我的研一下半学期是在家中度过的,孙老师建议我在完成学校的网上课程前提下,利用时间寻找自己的研究生课题。在选题的时候,孙老师要求我要积极思考,放开思路想具有先进学术性的问题,同时要与自己的兴趣结合才能在科研中富有激情,充满干劲。刚开始,我打算选择的课题方向是圆柱壳的几何缺陷问题,该问题的核心是屈曲问题,这也是我当时比较感兴趣的。但是,该问题对理论的积累要求很高,并且是否能提出有意义的创新点也不得而知。彼时的我很苦恼,没有任何科研经历的我是否能进行这样的一个课题?
2020年9月28号,研二开学快一个月了,我还是没能确定自己的课题,毫无进展的我感到有些迷茫,不禁对自己产生了怀疑。在这种情况下,孙老师为2019级硕士研究生精心挑选了4个来自学术前沿的课题并准备了相应的资料,这些课题非常适合我们这些“科研萌新”,课题内容方便理解又极具深度和研究价值。其中,我选择了“薄带形态转换”这个课题,其实关于“薄带形态转换”这个问题的相关资料,孙老师早在2019年薄带文章发表时将其就发到群里面让研究生们思考,可是我并没有足够的重视,没有给老师反馈,现在想想,如果一开始我就能重视这个问题,我便能非常早的开始我的科研。所以说,一定要重视老师发的所有科研问题,端正态度,积极思考,才能在科研中领先一步。“薄带形态转换”这个现象可以描述为:拿一张纸条,抓住两端,使之成拱形,当两端同时往里旋转时,纸条首先会偏转,然后跳跃,最后会快速翻转以返回到其先前的形状。如此来源于生活却又高于生活的研究,使我兴趣盎然。这便是我这趟学术旅途的起点,未来的四个月我都奋斗在这条充满挑战也充满希望的路上。
2020年10月初,为了快速地学习和理解“薄带形态转换”的问题,我根据孙老师的建议对原文献( Twist-Induced Snapping in a Bent Elastic Rod and Ribbon[J]. Physical Review Letters122(11)114301.1-114301.5)进行翻译。第一遍浏览原文献时,众多陌生的术语让我寸步难行,我清楚的知道,科研讲究严谨,只有准确理解原文献的内容,我的课题才能顺利进行下去。然后我沉下心借助词典及翻译软件查阅其中的陌生词汇、专业术语,对比各个语境下的释义,多次梳理文章内容,使自己完全理解原文献内容。收获与付出是成正比的,在这个翻译过程中,我不仅掌握了整个课题框架,同时也精炼了语言表述能力。

图1:纸条的形态转换过程
有了初步的知识积累后,我开始利用有限元软件ABAQUS对该问题进行仿真建模,在建模的过程中,由于对薄带的属性理解不足,以及选取的加载方式不正确,最开始的运行结果并不理想,在这里特别感谢宋广凯师兄和李翔同学在这个过程提供的帮助,李翔同学提供了重要的弹性材料PET和超弹性材料橡胶的本构关系,宋广凯师兄解决了分析中的收敛问题。当程序能成功运行,且最终得到的运动视频与原文献一致时,我的心情是十分喜悦的,并立即在例会上向孙老师展示了该成果并受到孙老师的鼓励,这也坚定了我继续前行的决心。但是,科研总是会先给你点甜头,再给你狠狠的一棒,喜悦的心情并未持续多久。我发现,模拟出的动画虽然与原文献里动画大致的变化一致,可如果对模拟的薄带中心点提取位移,却与原文献的实验数据差距较大。面前的科研路又变得模糊起来,我苦思冥想,几近绝望,整天看着模型,反复核对,却毫无进展,再次对自己产生了怀疑。俗话说,山穷水尽疑无路,柳暗花明又一村,盯了两天的模型后,我灵光乍现,如果我一开始运行的结果没错,说明有限元分析此问题肯定是可行的,而数据的偏差则可能由很多其他因素影响。对此,我对薄带的泊松比、弹性模量、扭转驱动加载的方式、单元的种类和数量、分析步的选择全部进行了优化,终于得出了有限元结果与实验结果吻合精度高的模型,我兴奋的差点跳起来,没有什么比这种完全靠自己取得的突破更能激励自己了。

图2:窄带的有限元-实验结果比较
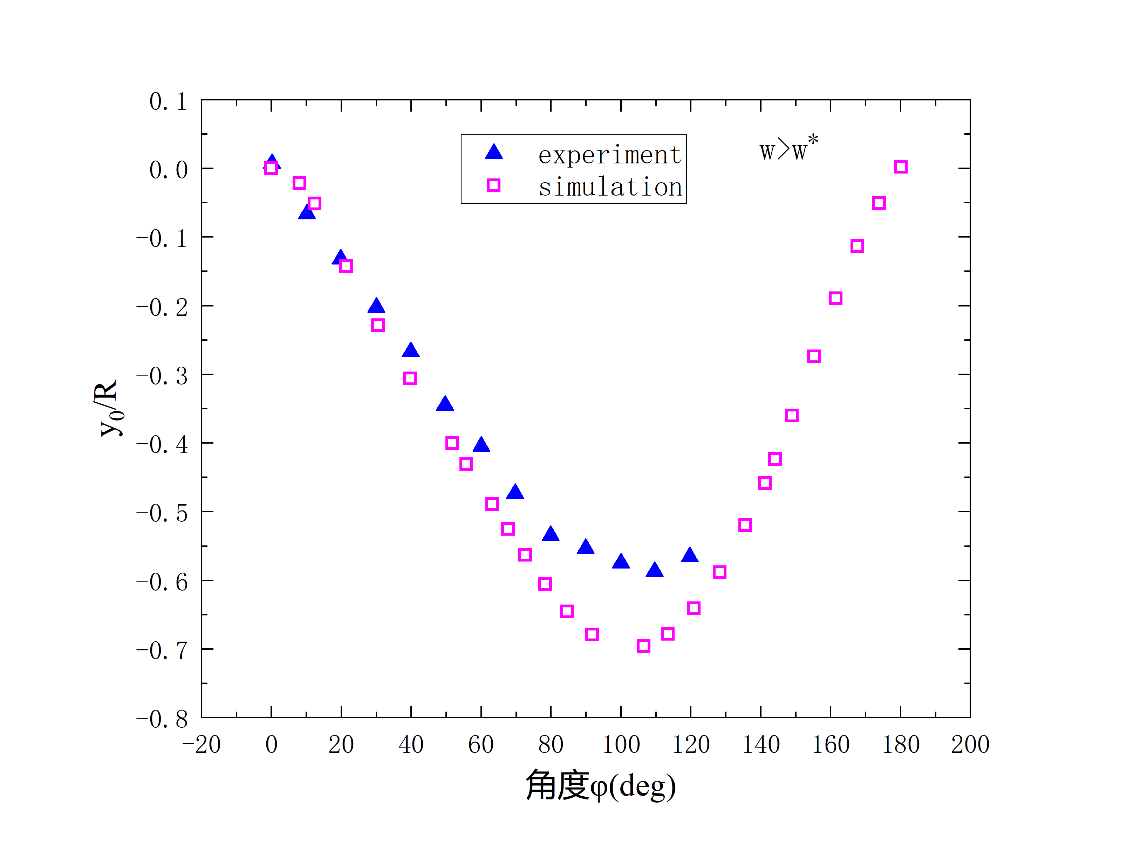
图3:宽带的有限元-实验结果比较
解决了模型问题后,才算初步在这条科研路上站稳了脚。继续往前走就不能仅仅满足于重现别人的结果了,一篇新的学术论文里要有自己的创新点。2020年11月,再次深度学习原文献后,我发现他研究中存在不完善的内容,并决定对此展开自己的研究。其中特别重要的是薄带形态转换的临界宽度问题,原文献采用实验结果拟合公式,实验数据较少导致结果不是太准确。而利用有限元程序却可以获得大量的数据,但是每一个数据都需要在有限元中重新建模,考虑到我准备将临界宽度精度提升到0.05mm,需要的模型数量成百上千,这会造成巨大的工作量,且会耗费大量的时间。一道新的难题摆在了我的面前,不解决这个难题,剩下的工作将难以进行。我迎难而上,通过各个渠道寻找解决办法,浏览了各种有限元网上论坛,向周围的同学取经。努力的人总是幸运的,在我艰难寻求解决办法的时候,孙老师转发了一条推送叫做“Abaqus Python渐进式二次开发”。恍惚间,一扇全新的大门好像对我打开了,Python 竟可专门解决此类大量机械化建模,我从来没有如此急切地想要学习一门知识。然后我在一周内利用网上教程和书本,经过高强度的Python学习后,终于编写出了模型的Python 脚本文件。当Python文件第一次顺利运行,并能够按我预期的计划提交分析任务时,我明白了成功只会青睐于有准备的人,只有付出才有回报,如果没有这次沉下心来踏踏实实地学习Python,那么这次科研有可能就止步于此。这次学习中收获的Python 建模知识不仅解决了此次的难题,也会对以后的研究起到帮助。这里要感谢张一同学与我进行关于Python 的学习交流,我们一起对最初的脚本文件进行修改,得到了运行更迅速和准确的脚本,还要感谢党文同学帮忙运行了部分模型,加快我科研的进程。孙老师一直强调,除了要有物理知识和理论修养外,研究生应当学习并掌握更多的软件工具,这是科研工作很重要的一环。上面我已经介绍了Abaqus和Python在我科研过程中起到的巨大作用,没有这两个最基本的工具我就不会取得任何成果。除此之外,我在这个科研过程中还学习了数学软件Maple,这是一个具有强大符号运算能力、数值计算能力、图形处理能力的软件,在我理论推导中起了无可替代的作用;还有画图软件Origin,具有强大的数据导入功能和绘图功能,我使用Origin绘制了论文中的大部分图形,还拟合了临界宽度的曲线,Origin实在是科研工作者工作必备的利器。
2021年1月,我终于完成了研究中所有的数值模拟。接下来就是对有限元的数据进行处理,结合数据绘制相应的图线,并开始构思论文的框架。在得到所有的数据图像后,我竟有些得意,想着在此基础上写一篇文章不是难事。可实际上,作为一名彻彻底底的“科研萌新”,对论文的逻辑、章节的内容填充、小标题的划分知之甚少,甚至图形的美观度这些学过的最基础的论文写作知识都忘得一干二净,还有重要的摘要、引言和结论部分,也基本上无从下手。有成果却不知道如何展示,心情无疑是十分憋屈的。向孙老师如实说明该情况后,孙老师考虑到我们是初次写作学术论文,给我们推送了关于如何写作学术论文各个部分及包含哪些要点的文章。孙老师带来的这些资料毋庸置疑就是我科研路上的指路明灯,我按着上面的内容,一步一步老老实实地推进着自己的首篇学术论文,终于在2021年1月25号完成了论文的第一稿。
2021年1月底由于手术我中断了这篇文章的写作,出院后我便立即向孙老师展示了论文第一稿。孙老师浏览后认为文章里面缺少理论基础,需要对其进行补充,才能形成一篇结构完整的学术论文。我悉心听取了老师的建议,开始对薄带结构的理论部分进行学习。由于之前研究重点都是数值模拟方面,学习中忽略了薄带结构的理论推导部分,首要的难题就是理解理论中的符号概念,例如欧拉角、旋转速率、欧拉-拉格朗日方程等等;其次就是推导各符号的关系,得到自己想要的数学模型;最后便是整理,将别人的结果和自己的结果区分开,在论文中集中展示自己的成果,即扭转驱动下薄带的动力学模型,以及薄带在运动中欧拉角随弧坐标和支座转角的变化。这个过程描述是很简单的,但实际上理论的学习往往相伴着枯燥,大部分时间我都是在研究那几个公式,经常会持续好几个小时。可是一旦有突破,便会瞬间打起精神,这大概就是科研生活的真实写照吧。
2021年2月的最后一周,对我来说意义非凡。这一周孙老师就我的论文内容与我开了四次学术交流会。第一次会议中孙老师看了文章指出论文的摘要和前言需要重新书写,关于摘要,需要介绍清楚研究主题、方法和目的,最后要给出结论和研究结果的意义,同时要言简意赅,突出重点,某些特别无足轻重的点可以一笔带过;关于前言,这一部分的逻辑很重要,孙老师一步一步地帮我确定了引言的逻辑,以及如何介绍研究背景,如何引出研究内容,每一部分的内容如何过渡,过渡的时候如何突出中间的联系,孙老师都详细地为我解答。孙老师强调道:文章的中文表达一定要流畅,不能出现表达性的错误。除此之外,孙老师还建议我在前言开头里添加纸条运动的图像,用于开门见山地介绍本文研究内容。第二次会议孙老师在我第一次修改的基础上提出了对于题目的修改意见,应该更贴合文章的研究内容,建议修改为“拱形薄带在扭转驱动下的形态转换问题”,这对我来说无疑是醍醐灌顶的,孙老师建议的这个题目简明扼要,可以让阅读者一眼就了解到论文的中心内容。关于正文,和前言类似,逻辑很重要,同时还需要对各个章节的内容进行仔细检查,要合理的运用文章的小标题,尽量不要在一个章节堆叠太多内容。孙老师还仔细地浏览了我的理论推导部分,强调了数学表达的准确性,指出某些公式中的偏微分算符应该修改成常微分算符,并建议我用双曲函数来描述公式里的相关内容。孙老师的这个建议极大地简化了我的公式,让我意识到了加强数学修养的重要性,不管研究什么问题,扎实的数学知识都能够提供有效的帮助。第三次会议孙老师建议我增加有限元结果和理论结果的比对,这会使论文的结论更加有说服力。孙老师还提到文章的公式需要进一步地推导,结论部分尚需完善,并教导我说结论不能是文章的摘要,不要照抄正文部分,只需要提取最关键的内容进行展示,要具有足够的概括性。最后一次交流会孙老师再一次对全文进行了审阅,强调了文章中的符号表达一定要准确,如果文章中出现别人的研究内容一定要注明引用,不能剽窃,要实事求是,端正作科研的态度,不要有小心思。最后孙老师提出了一些细节上表达的改动。事实证明,这种密集的会议对效率的提高是十分明显的,短短的一周便让我完成了从初稿到终稿的过程,这当然离不开孙老师在这几次会议中孜孜不倦地引导,正是孙老师提出了许多关键性的修改意见,给了我很大启发,让我顺利完成这篇文章。
中文定稿后,我花了大量时间将其翻译成英文稿件,在这个过程中借助了一些翻译工具,也有自己的仔细校对和斟酌语句,尽量最大程度地完善这篇英文稿,这里面对英文水平的提高也是显而易见的,完成英文稿后,在孙老师的建议下,我将文章交由letpub润色,润色修改返回后便开始了投稿,在投稿的过程中,尽管已经检查了许久并借鉴了之前几位同学的投稿经验,但百密难免一疏,仍是出现了因为自己粗心大意导致的错误,其一是上传的总文件中没有打开参考文献bib的格式文件,导致无法将参考文件打开,这种格式问题错误是非常低级且需要反思的,其二是投稿文件中的图片没有标明出编号,这种错误十分的不严谨,也使孙老师在重新填写编号中消耗了大量本该避免的时间。这些错误完全是不应该发生的,都是因为自己的粗心大意浪费了孙老师的很多时间,将这些错误罗列于此,希望时刻提醒自己做事一定要认真认真再认真,也希望其他同学引以为鉴,不要出现类似错误。
一开始我投稿的期刊是《Journal of the Mechanics and Physics of Solids》和《International Journal of Solids and Structures》,但被告知与期刊内容不符而退稿,幸运的是,这些期刊处理文章的时间很快,并没有浪费太多的时间成本;随后,我在孙老师的推荐下投递了《Thin-Walled Structures》,现在回想起来,文章能顺利发表离不开孙老师选择的好期刊,我的研究内容与该期刊的主题十分契合,孙老师高屋建瓴的大局观避免我走了很多弯路。
2021年4月23日,这是文章投出去的日子,到7月14日,文章的审稿意见返回;那一天早上我一睁眼,打开手机,看见了孙老师在凌晨两点发来的消息,一方面我开心于审稿人对文章研究内容的支持,另一方面我又钦佩于孙老师在科研上努力钻研、不舍昼夜的精神;当时,孙老师还让我上午十点前往他家中讨论论文事宜,最开始我担心孙老师会不会因为没有足够的休息时间而有所疲惫,可现实恰恰相反,孙老师神采奕奕,为我指出了回复审稿人意见时需要注意的要点,文章哪些部分还需要改进,以及还需要增加哪些内容,还建议我详细阅读审稿人推荐的文献。接下来一个月的时间我按照审稿人和孙老师的意见对论文进行了修改,并对审稿人的意见逐一回复,在8月5日将论文修改稿重新交由孙老师审阅。这时出现了令我意想不到的情况,孙老师仅仅是瞥了一眼,就发现了论文公式中一个致命的错误,即泊松比的取值为-1,这在薄带结构中显然是不正确的,而泊松比在正常范围取值时,得到的解只有虚数解,这显然也是不对的,于是孙老师让我对论文的公式进行重新推导。那周周末我重新学习了欧拉-拉格朗日方程,从文章最开始的原始公式出发,最后得到了含3个的微分方程的方程组,其中有三个未知量,我将方程组输入到maple程序里,却发现不管使用怎样的边界条件,方程都是无解的,接下来我尝试了许多方法,结果依然如此;当时,在我已经没有其他办法时,孙老师再一次为我提供了巨大的帮助,在此前的尝试中,泊松比取值正常范围时方程解为虚数,这一次,孙老师亲自推导方程并编写maple程序求解,引入了两个无量纲量分别代替自变量和因变量,改动并不大可结果却完全不一样,我们在0到0.5内取了不同的泊松比进行测试,结果都是实数,至此,困扰我的问题在孙老师的帮助下解决了,我又一次被老师强大的数学功底所折服。回想此次出现的公式危机,我意识到我之前的数学基础和物理常识实在薄弱,而且在公式推导上没有沉下心来,习惯只看头和尾,最重要的推导过程却忽略了,这一次有老师提醒所以侥幸过关,那么以后呢,做科研的核心还是要靠自己,只有自己不断补充相关知识,不停吸收学术养分,脚踏实地,才足以仰望美丽的科研星空。
过了公式这一关,在老师的审查下,还发现了论文中很多简单但不可忽略的错误,我将错误罗列下来,希望研究院同学引以为鉴:论文公式中符号的表达一定要正确,如有矢量推荐使用英文黑体;表格按照期刊要求进行绘制;图片中区分不同组数据建议采用不同线型;表格和图片的编号一定要准确;公式表达正确的同时要做到美观;修改稿要有两种版本,即红色修订版和正常版;注意期刊对图片格式的要求,有些期刊要求图片格式为eps格式;LaTeX中去掉多余的符号和空行,使整个文件显得干净整洁;文章中所有的符号用两个$隔开加以区分。以上就是在我文章中发现的问题,望研究院同学在自己的论文写作中不要再犯同样的错误。最后于8月19日将修改稿和答审稿人意见返回至编辑部。
同样是凌晨,10月1日孙老师告知了我文章录用的好消息,这对我来说便是最好的国庆礼物了,一时间除了感谢竟想不出其他言语。回顾这次科研的整个过程,我百感交集,有痛苦和疲惫,也有近乎“案牍劳神",但更多的是灵光乍现时的兴奋和收获成果时的喜悦。论文的顺利录用,离不开孙老师的诲人不倦,离不开研究院同学的倾囊相助,也离不开自己一点一滴的努力。在此,我要再次隆重感谢孙老师在本文的选题、构思和撰写等方面给予的指导与帮助,同时也是孙老师在论文的修改上给予了许多宝贵的建议,才使我的论文得到了不断的完善,乃至终于录用。感谢孙老师,感谢提供帮助的每一位同学。
以上内容均为本人此次科研经历的真实记录,包含了我从完全不懂科研到可以自己独立撰写文章的全部内容,希望研究院同学可以加以借鉴。
论文已发表在《Thin-Walled Structures》上,该文第一作者为2019级硕士研究生戴远帆,第二作者为2019级硕士研究生张一,第三作者为2019级硕士研究生李翔,通讯作者为孙博华院士。
文章链接:Y.F. Dai, B.H. Sun, Y. Zhang, X. Li, Morphological transformation of arched ribbon driven by torsion, Thin-Walled Structures 170 (2022) 108511,https://doi.org/10.1016/j.tws.2021.108511