孙博华院士:对湍流雷诺平均方程(RANS)的重新考察


湍流现象无处不在,其定量理解号称是经典物理的一个难题。量子力学创始人之一海森堡就曾经说过:我要带着两个问题去见上帝:量子论和湍流。我相信上帝只对第一个问题有了答案。
英国科学家 Osborne Reynolds 分别于1883年和1895年发表了二篇湍流研究著名论文,开启了湍流问题的科学研究。Reynolds 在1895年的论文中,提出流场量可以分解成平均场和脉动场的矢量和(称为Reynolds分解)。利用Reynolds分解可以把流体力学的Navier-Stokes 方程组和能量方程改写成Reynold-averaged Naviers-Stokes equations(RANS) (雷诺平均方程组)。由于平均方程组非常复杂,人们为了简化就忽略了关于脉动场的方程组,从而造成了“不封闭”的问题。
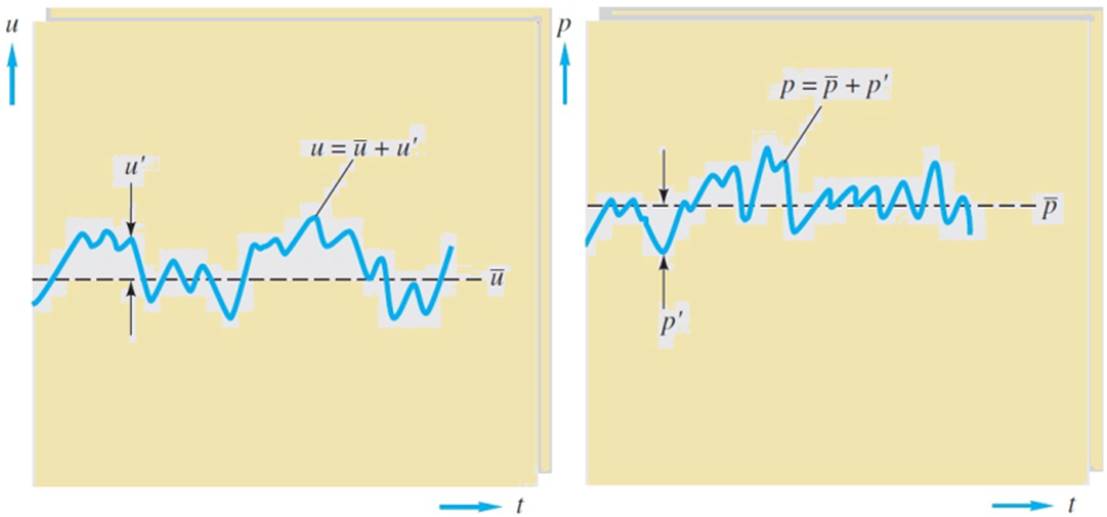
图1 速度分解和压力分解
针对湍流研究一百多年来没有多少本质进展的困境,作者敢于把目光越过所有先代学者的伟大成就,直接回到130年前Reynolds研究湍流的起点,重温 Reynolds 的湍流原点思想,以期获得对湍流RANS方程的深刻理解。
目前的文献对于雷诺方程认为:RANS方程的个数只有四个,而未知函数却有十个,即
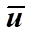 ,p及六个雷诺应力分量。为了使方程组封闭,必须在Reynolds应力张量及平均速度之间建立补充关系式。
,p及六个雷诺应力分量。为了使方程组封闭,必须在Reynolds应力张量及平均速度之间建立补充关系式。
孙博华院士指出,Reynolds(雷诺)应力张量不是一个一般2阶对称张量(有6个独立分量),而是一种特殊的二阶对称张量
 ,即其分量是3个脉动速度分量的两两乘积的时间平均。对于三维问题,有3个速度脉动分量
,即其分量是3个脉动速度分量的两两乘积的时间平均。对于三维问题,有3个速度脉动分量
 ,其两两乘积可以产生9个组合,由于乘积的可交换性
,其两两乘积可以产生9个组合,由于乘积的可交换性
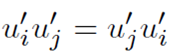 ,即对称性,这9个组合中就只有3个脉动分量是未知量。所以,Reynolds(雷诺)应力张量的9个分量只有三个未知脉动速度分量是未知量,而不是6个未知分量。
,即对称性,这9个组合中就只有3个脉动分量是未知量。所以,Reynolds(雷诺)应力张量的9个分量只有三个未知脉动速度分量是未知量,而不是6个未知分量。

孙博华院士给出了使用张量整体表达的RANS方程组,推导出了湍流转捩的临界雷诺数:
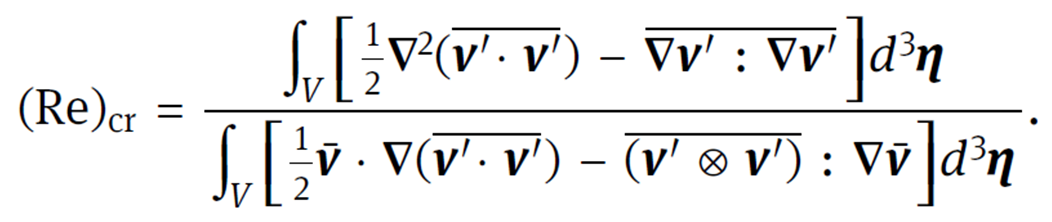
本研究在Reynolds原创思想的框架下,研究了湍流分析中的一些基本问题,如雷诺应力张量分量的未知数个数问题和湍流转捩的临界雷诺数等,所得结果有助于对于湍流现象的进一步理解。
研究成果发表在《Open Physics》, 孙博华院士是唯一作者:
Bohua Sun, Revisiting the Reynolds-averaged Navier–Stokes Equations, Open Physics 2021; 19: 853–862.
https://doi.org/10.1515/phys-2021-0102
https://www.degruyter.com/document/doi/10.1515/phys-2021-0102/html