2021年,力学技术研究院院长孙博华院士分别在国际著名学术期刊《Thin-Walled Structures》(薄壁结构)和《International Journal of Non-Linear Mechanics》(国际非线性力学杂志)发表3篇研究性论文,系统分析了环壳结构,得到了圆截面薄环壳的小变形精确解,并发展至斜椭圆环壳,以及解决了Gol’denveize与Flügger提出的两个壳体难题。
环壳(图1)是中国现代力学的二位奠基人钱伟长和张维都做过系统研究的唯一的一种壳体,环壳作为规则壳体中最复杂的一项,其基本方程是变系数的高阶偏微分方程。有关环壳的最早研究是从德国亚琛工业大学开始的,开创环壳研究的是Hans Reissner。Hans Reissner于1912年受母校柏林工业大学召唤担任工程力学教研室主任。张维先生作为研究环壳的第一位中国人,在柏林工业大学该教研室攻读博士学位,其环壳的研究可以说是从这类壳体研究的源头开始。

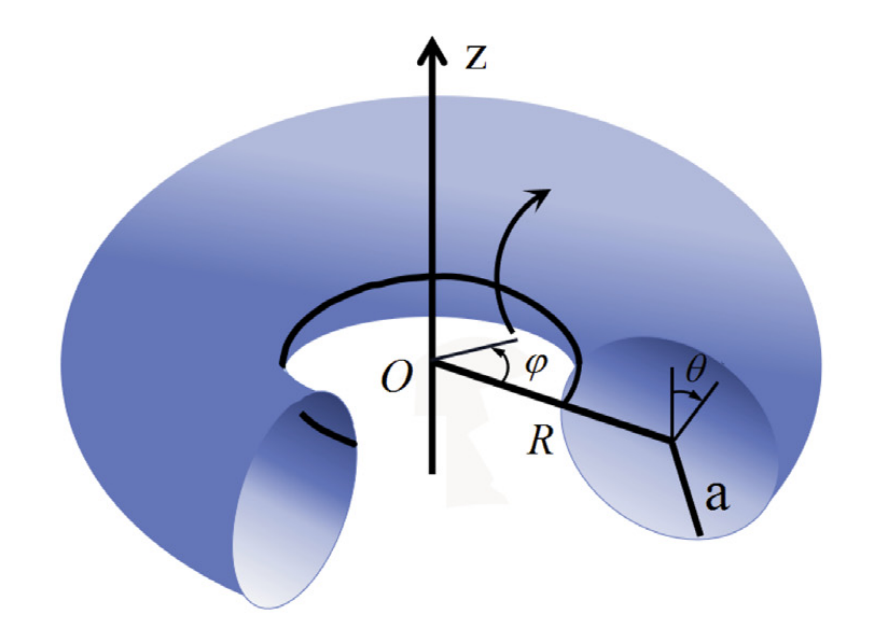
图1 环壳的几何图形
环壳结构的高阶偏微分方程,其系数是分数型的且分母在其两个几何顶点有“零点”,即具有奇异性,由于在顶点两边的高斯曲率变号而使方程变性(图2),是壳体理论中最复杂的问题之一。
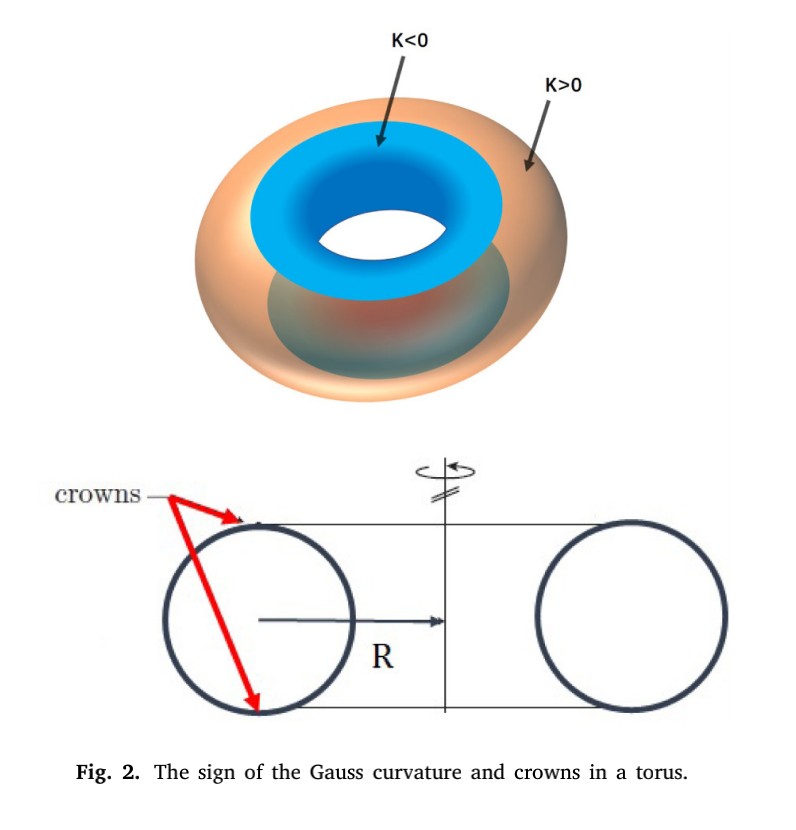
图2 环壳的高斯曲率变化
圆截面薄环壳的小对称变形

Novozhilov于1959得到了对称变形环面的复形控制方程。但该方程十分难以求解,钱伟长先生得出了轴对称细环壳的一般解,而更加一般的情况,尚未有人给出较好的结果。
为解决上述方程式,我们引入变量变换,得到了是一个具有四个正则奇异点的傅氏型微分方程,其解可以用Heun的函数来表示。为了进一步计算,解必须分解为实部和虚部,但由于Heun函数的复杂表达式,这在分析上是不可能的,即无法得到环面的力、力矩和位移的解析分量。为此,我们将耦合微分方程系统解耦成四阶微分方程,提出了一种实形微分方程系统,并利用Maple写出了相关数值求解的一般代码。通过有限元模拟与Hans Reissner’s方程对本文结果进行了验证图(3)。
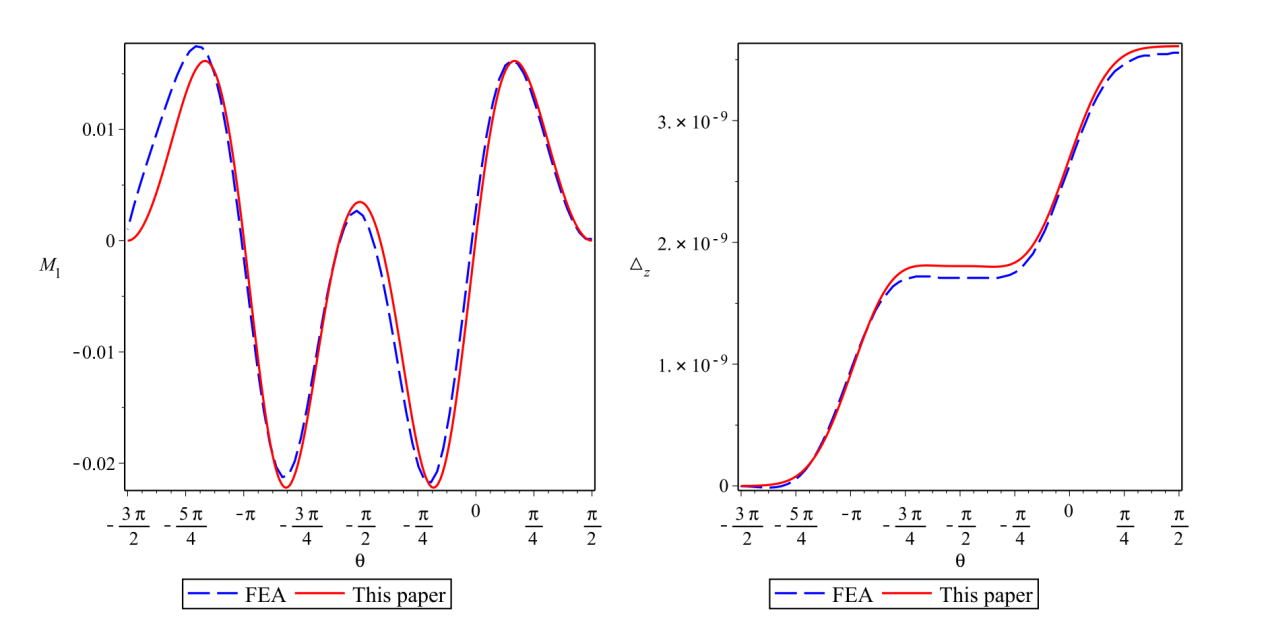
图3 有限元模拟验证
研究表明,弹性环面的变形和应力响应都对半径十分敏感。且在壳理论的历史上,发展了一种膜理论来简化壳结构的分析。在对壳元平衡的研究中,该理论忽略了所有的弯曲。以上案例研究表明,壳体无矩理论不能在环面曲率的强烈变化时,提供了合理的结果(图4)。
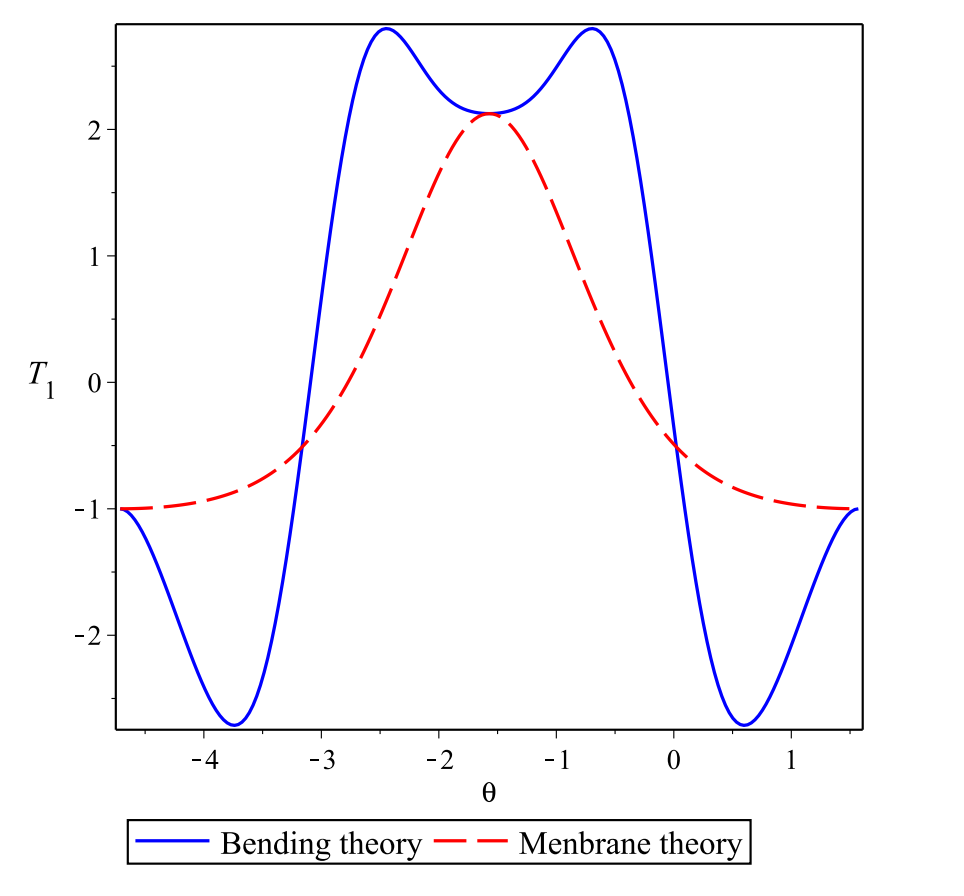
图4 壳体弯曲理论与薄膜理论对比
弹性环壳从圆形到斜椭圆截面的几何诱导刚度

著名力学家,德国的Wilhelm Flügger于1934年出版了有关壳体的第一部专著,其于1973年出版的专著“Stresses in Shells”中所提及的问题,即无矩理论结果下,剪力无法传导(图5)。在我们研究弹性环壳从圆形到斜椭圆截面的几何诱导刚度中,该问题使用弯曲理论代替无矩理论时被解决。

图5 Flügger问题
在环壳结构的刚度研究中,我们发现环壳横截面几何形状的变化将诱导结构刚度改变,其中最简单的例子是鸡蛋的侧面比尖端更容易破裂。针对这个问题,本文重点研究了弹性环壳的几何诱导刚度,并研究了从正椭圆到斜椭圆环壳的刚度变化(图6)。

图6 斜椭圆环壳几何构型
而对于斜椭圆环壳的力学问题,其难点在于如何寻找斜椭圆环壳的主半径。斜椭圆环壳可视为一个围绕其中心旋转β角的正椭圆环壳,据此我们第一次推导出斜椭圆环壳曲率半径(图7)。
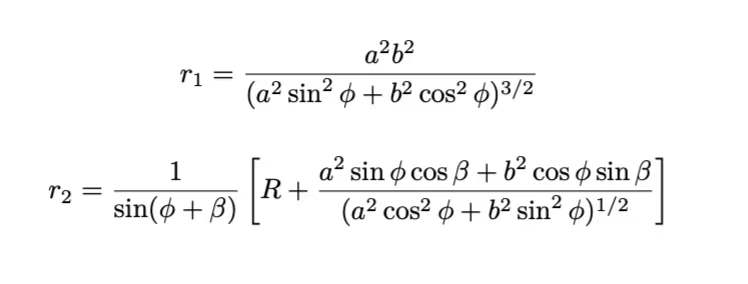
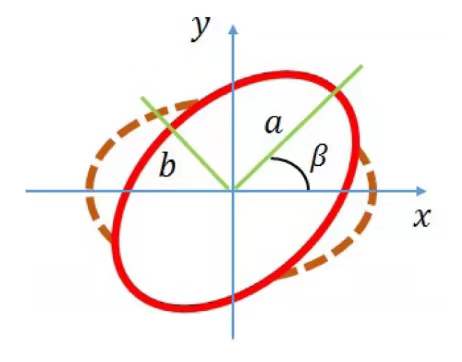
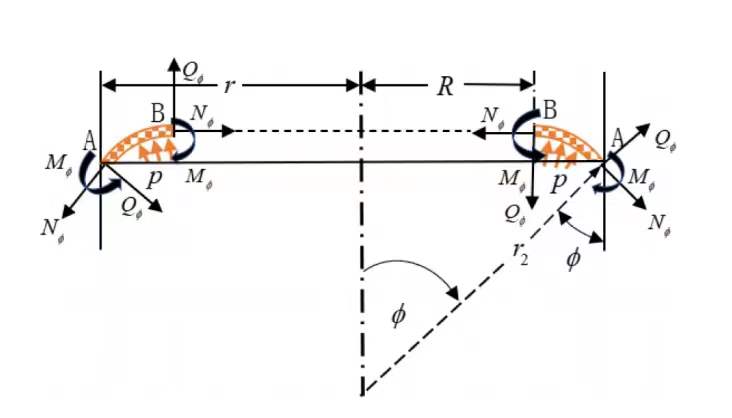
图7 斜椭圆环壳演化过程
在面对已有的Reissner–Meissner或者Novozhilov的复杂控制方程,其均存在不能用于振动与非线性问题的局限性。为此,我们给出了一个关于位移的六阶常微分非线性方程系统,并对其进行了数值研究(图8)。
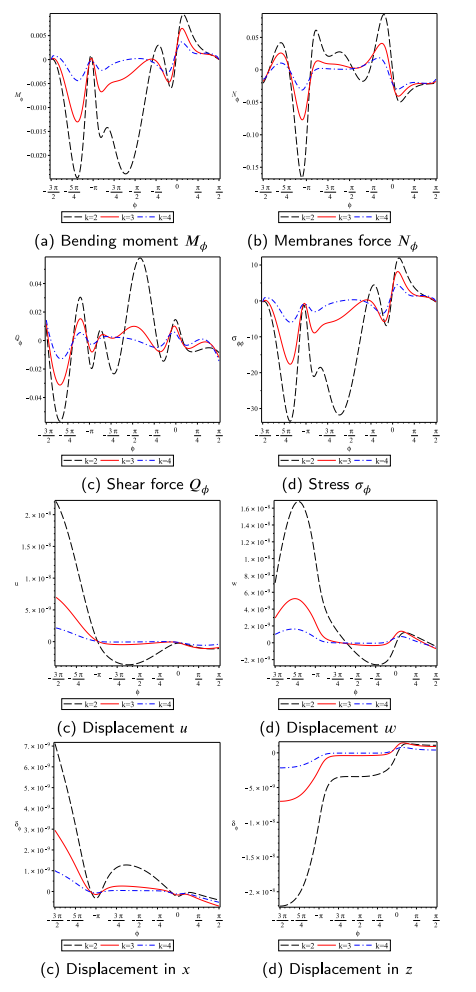
图8 斜环壳刚度变化结果
数值模拟结果显示环壳的变形和应力响应对半径比都十分敏感。同时内环因具有负高斯曲率,比外环刚度更高。同时,斜角对椭圆环壳的力学有较大的影响,且较小的角度偏差会显著影响变形和强度分布的变化。此外,环壳以一种非常特殊的方式变形,其应变和应力集中在两个非常狭窄的区域,即在顶部和底部的皇冠周围。环壳的这种性质对于材料胞元设计十分有用,其中通常需要具有负高斯曲率的较强单元。同时,通过对高斯曲率的控制,亦可控制其刚度变化。
弹性环壳的Gol’denveizer问题

在面对环壳长期未解决的Gol’denveizer问题,即无矩理论因皇冠处的应力发散,无法预测这个变形。虽然Audoly和Pomeau(2002)基于添加了非线性边界层的壳体的无矩理论对该问题进行了研究,但该问题仍远未得到解决。基于薄壳的弯曲理论框架,我们提出了环壳的Gol’denveizer问题解决方法(图9)。
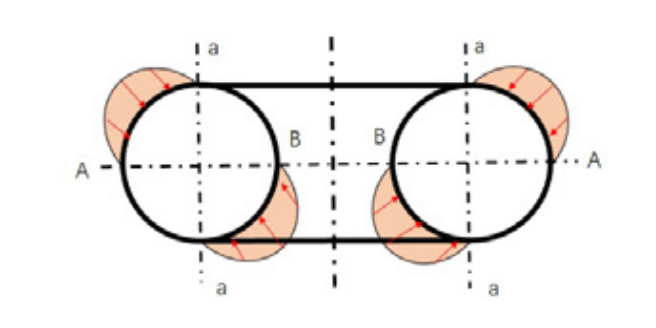
图9 Gol'denveizer问题
首先,我们针对旋转壳对称位移复杂公式进行了分析,而其中最为关键的是,正确给出相应的边界条件。在结合边界条件的周期性,我们得出了相应的可用于数值求解的实形微分方程系统。在此基础上,利用Maple进行数值求解(此数值结果使用有限元进行验证)。结果显示,我们所使用的壳体弯曲理论能非常好的解决皇冠处应力发散问题,而壳体无矩理论由于环壳拓扑结构影响,在皇冠处没有弯曲能力,无法传导剪力(图10)。
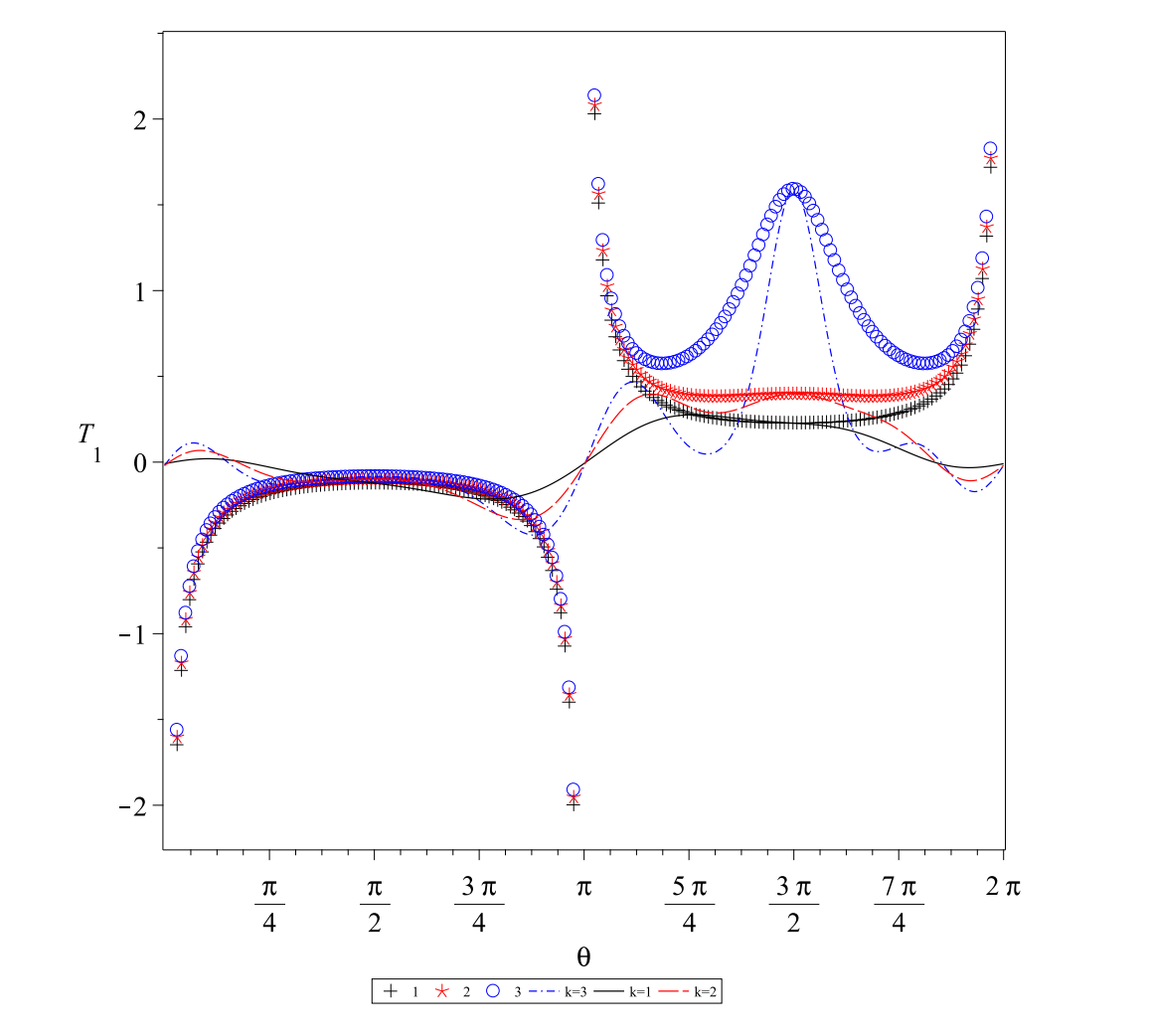
图10 壳体弯曲理论与无矩理论结果对比
结果显示环壳的变形和应力对半径比十分敏感,而只有基于壳层的弯曲理论才能充分理解环面的Gol’denveizer问题(图11)。
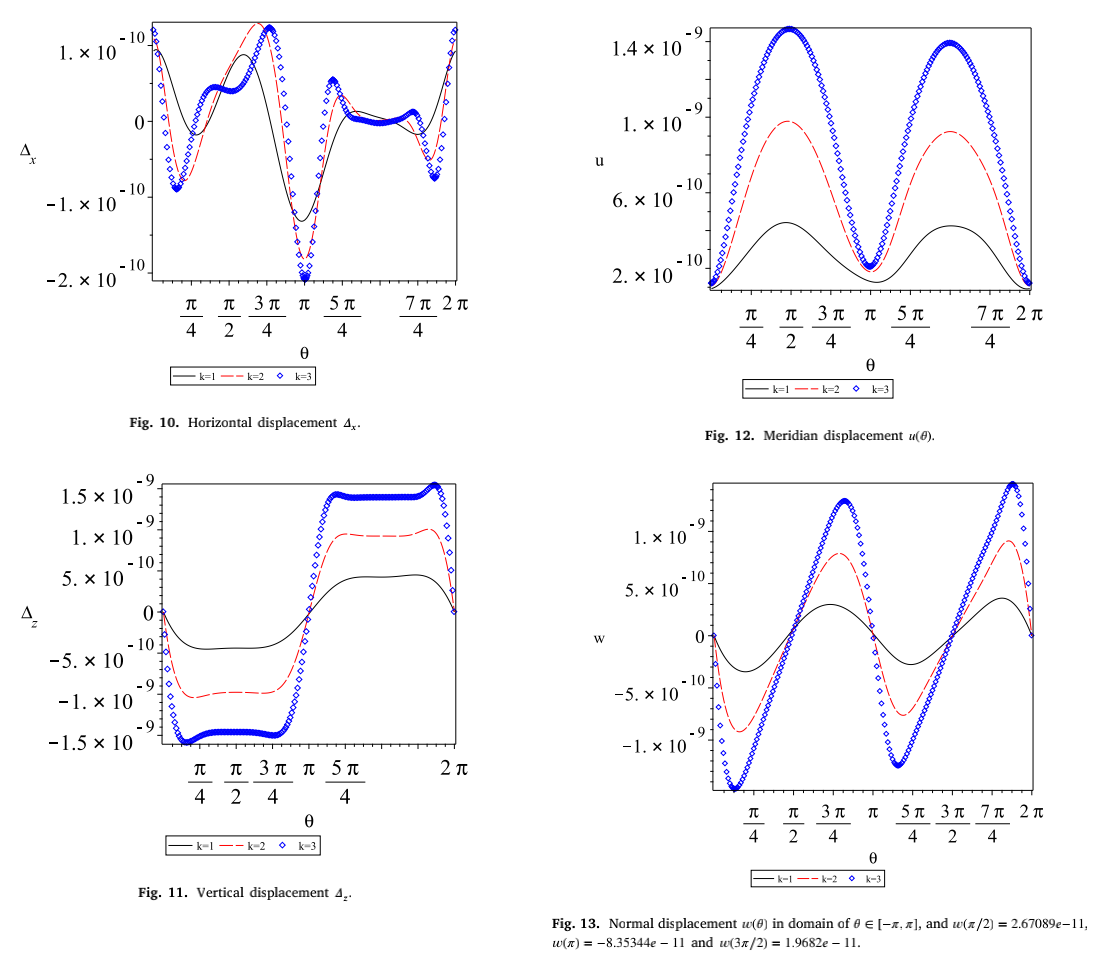
图11 半径比影响
最后值得注意的是,所使用求解的函数实部是一个保型函数,其大小半径比成正比,这可能意味着该函数(图12)与环面几何之间存在某种深刻的联系,这应该在将来进行研究。
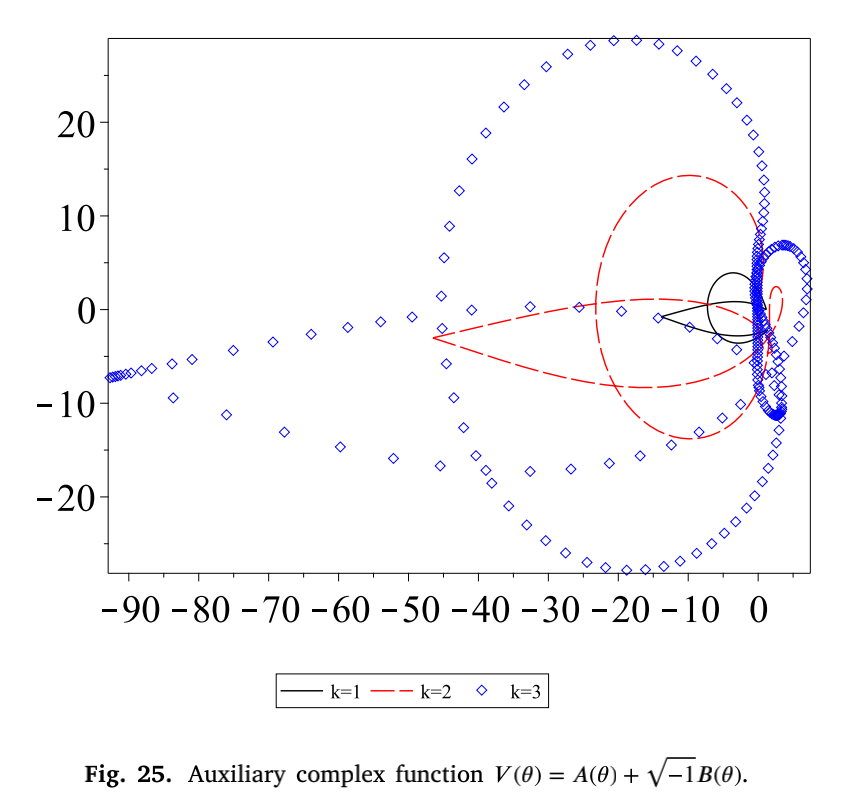
图12 辅助复杂函数
《International Journal of Non-Linear Mechanics》2021年影响因子为2.985,中科院分区3区期刊,《Thin-Walled Structures》2021年影响因子为4.442,中科院分区2区期刊。这3篇论文均以西安建筑科技大学为第一完成单位,孙博华院士为这些论文的唯一作者。
文章链接:
[1] B.H Sun,Small symmetrical deformation of thin torus with circular cross-section, Thin-Walled Structures, 163(2021)107680.https://doi.org/10.1016/j.tws.2021.107680
[2] B.H Sun, Geometry-induced rigidity in elastic torus from circular to oblique elliptic cross-section, International Journal of Non-Linear Mechanics, 135(2021)103754.https://doi.org/10.1016/j.ijnonlinmec.2021.103754
[3] B.H Sun, Gol’denveizer’s problem of elastic torus, Thin-Walled Structures. 171(2021)108718. https://doi.org/10.1016/j.tws.2021.108718